発表のポイント
◆ 量子情報処理の多くに不可欠である量子擬似ランダム性が、物理学における中心的概念の1つである対称性によって受ける影響を世界で初めて解明した。
◆ 対称性を満たす量子擬似ランダム性を効率的に生成する量子回路の構成方法を提案した。
◆ 物質固有の対称性を活用した効率的な量子情報処理手法の開発や、量子物理学をはじめとする基礎科学における新奇現象探索の発展に繋がると期待される。
対称性を満たす量子擬似ランダム性のイメージ図
概要
東京大学大学院工学系研究科物理工学専攻の三橋洋亮大学院生、吉岡信行助教らは、対称性(注1)を満たす量子ランダム性(注2)の擬似的な生成方法を明らかにしました。対称性を考慮しない場合の擬似的な量子ランダム性の発生方法については以前から知られていましたが、本研究ではその手法が対称性を考慮した場合にも適用可能であるかという未解決問題を解決しました。具体的には、対称性の条件を加えても擬似ランダム性のレベルが保たれるような対称性のクラスを完全に特定しました。また、その時に対称性を満たす擬似ランダム性を無駄なく生成する手法も発見しました。本研究は、対称性に起因する新たな物理現象を解明するための理論的基盤となるとともに、物質固有の対称性を活用したより効率的な量子情報処理手法の開発に寄与すると期待されます。
発表内容
【研究背景】
量子的なランダム性は、基礎的な物理現象の解明から、量子コンピューターを用いた情報処理に至るまで、現代の物理学・計算科学・情報科学にわたる広範な分野において活用されています。完全な量子ランダム性の生成には莫大な計算時間を要するため、実用的には擬似的な量子ランダム性で代用されることが多く、その代表例としてクリフォードゲート(注3)と呼ばれる量子的な操作の組が挙げられます。近年では、物理学の重要な概念である対称性がさらなる豊かな数理構造・工学応用・物理現象を創発するものとして注目されています。一方で、対称性が量子擬似ランダム性にもたらす影響を数学的に記述する方法は知られておらず、また、対称性を満たす擬似ランダム性の生成方法も未解決でした。
【研究内容】
本研究では、1つ目の成果として、量子擬似ランダム性が対称性の下でどのように変わるかを明らかにしました。具体的には、クリフォードゲートの組の持つ擬似ランダム性のレベルが保存されるための条件は、対称性がパウリゲート(注4)を用いて記述されることであることを証明しました。このことは、擬似ランダム性のレベルに応じて定まるランダム性指標を計算することによって検証することもできました(図1参照)。
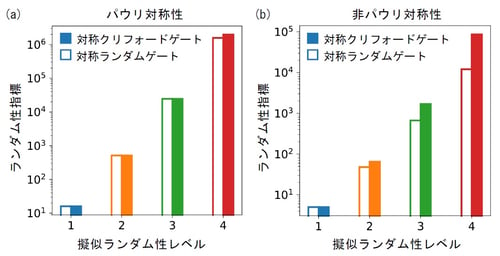
図1:擬似ランダム性のレベルに応じたランダム性指標の計算結果
クリフォードゲートの組が持つ擬似ランダム性のレベルは、導入される対称性が(a)パウリゲートで表される場合には保存される一方で、(b)パウリゲートで表されない場合には保存されないことを示しています。
さらに、2つ目の成果として、対称性を満たす全てのクリフォードゲートを無駄なく生成する方法を発見しました(図2参照)。この方法を使わずに対称性を満たすクリフォードゲートを得る従来の方法は、クリフォードゲートを大量に生成して、その中から低い確率で出現する対称なゲートを選び出すという非効率的なものでした。その一方で、今回発見した方法は、確実に対称性を満たすクリフォードゲートを得られるだけでなく、全てのゲートを等しい確率で生成できるという利点があります。
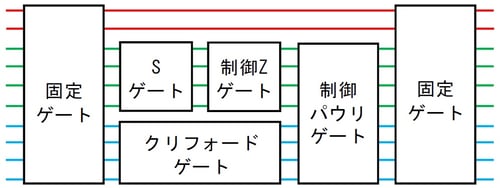
図2:対称性を満たすクリフォードゲートを生成する量子回路
対称性の種類により決まる両端のゲートに挟まれた4種類のゲートを変えることで、全てのゲートを等しい確率で生成でき、量子擬似ランダム性を満たします。
【研究の意義、今後の展望】
本研究は、対称性と量子ランダム性という物理学における2つの重要な概念に関わる研究のための理論的基盤を確立したという基礎的な意義を持つだけでなく、対称性を満たす量子ランダム性を擬似的に効率良く発生させる方法を明確に示したという実用的な意義も持ちます。本研究結果は、対称性に起因する新たな物理現象の研究や、物質固有の対称性を活用した効率的な量子情報処理手法の開発に役立つことが期待されます。
発表者・研究者等情報
東京大学大学院工学系研究科物理工学専攻
三橋 洋亮 博士課程/東京大学特別研究員
吉岡 信行 助教
論文情報
雑誌名:PRX Quantum
題 名:Clifford Group and Unitary Designs under Symmetry
著者名:Yosuke Mitsuhashi*, Nobuyuki Yoshioka
DOI:10.1103/PRXQuantum.4.040331
研究助成
本研究は、科学技術振興機構(JST)さきがけ研究「量子並列回路を用いた計算基盤の構築(課題番号:JPMJPR2119)」、JST ERATO「沙川情報エネルギー変換プロジェクト(課題番号:JPMJER2302)」、JST 共創の場形成支援プログラム「量子ソフトウェアとHPC・シミュレーション技術の共創によるサスティナブルAI研究拠点(課題番号:JPMJPF1234)」、日本学術振興会(JSPS)特別研究員奨励費「対称性、エンタングルメントと熱力学のリソース理論(課題番号:JP23KJ0421)」、東京大学統合物質・情報国際卓越大学院(MERIT-WINGS)、IBM Quantumの支援により実施されました。
用語解説
(注1)対称性
ある物質が対称性を持つとは、その物質に対して何らかの操作を行っても不変であることを表します。例えば、鏡に映しても不変である物質は鏡映対称性を持つと言います。量子力学における対称性は量子的な操作に関する不変性によって表されます。
(注2)量子ランダム性
量子ランダム性とは、量子的な操作をランダムに発生させることを表します。量子的なランダム性は古典的なランダム性よりも遥かに実現が困難であることが知られています。
(注3)クリフォードゲート
クリフォードゲートは量子ランダム性を擬似的に生成する際によく用いられるゲートです。その理由としては、クリフォードゲートによる量子状態の変化は古典コンピューターを用いて効率的に計算できることが挙げられます。
(注4)パウリゲート
パウリゲートとは量子力学における最も基本的な種類の操作です。具体的には、古典ビットの量子的な対応物である量子ビットを単位球面上の点として表現した時、各量子ビットに対するパウリゲートはこの点をx、y、z軸の周りに180°回転させる操作を表します。
プレスリリース本文:PDFファイル
PRX Quantum:https://journals.aps.org/prxquantum/abstract/10.1103/PRXQuantum.4.040331
おすすめ記事
本件に関連する記事はこちら

量子ランダムネスの生成速度の普遍性を証明 ―頑強で効率的な量子情報処理の実現に向けて―

理想的な乱数実現へ ―「パリティ対称性」利用が有効―


