本研究成果のポイント
・原子核の崩壊のタイミングは量子現象として本質的にランダムなものだと予想されており、これに基づく乱数生成の方法が提案されていますが、そのランダム性と秘匿性(注1)の厳密な証明はなされていませんでした。今回の研究は、核崩壊がパリティ対称性(注2)を持つ場合には、これらの証明が可能であることを示したものです。
・この研究は、量子の確率性と並んでパリティ対称性という物理学の原理的な性質が、理想的な量子乱数生成の実現に重要な役割を果たすことを示すものです。従来は関係性が薄かった量子情報と素粒子・原子核物理分野の間に、新たな連携の可能性を切り拓くものになっています。
【概 要】
高エネルギー加速器研究機構(KEK)素粒子原子核研究所・理論センター量子基礎論グループの筒井泉特別准教授は、三菱電機株式会社情報技術総合研究所の鶴丸豊広主席技師長、東京大学大学院工学系研究科物理工学専攻の佐々木寿彦講師との共同研究において、パリティ(3次元空間の反転に対する)対称性を持つ原子核の崩壊現象から生成される量子乱数のランダム性と秘匿性に、厳密な証明を与えることに世界で初めて成功しました。
原子核の崩壊現象を乱数生成のために利用する試みは、以前から(パリティ対称性を考慮しない方式で)進められてきたものですが、今回のパリティ対称性に基づく放射方向の測定を組み込むことにより、信頼性の保証された小型の乱数生成器の実用化が期待できることになります。
なお、この研究成果は、Communications Physics誌に7月1日付でオンライン掲載されました。
【背 景】
今日の社会生活を支えている情報通信の秘匿性や金融決済での認証の信頼性は、当事者間の暗号鍵(注3)の共有により保証されています。その暗号鍵には何らかの方法で生成した乱数が使われますが、これには一定のアルゴリズムに基づいて生成した疑似乱数が用いられるのが標準的です。しかしながら、これは真の意味での乱数ではないため、盗聴者が続く数字の並びを予測できる可能性があり、解読アルゴリズムの進展により将来的に暗号鍵が解読される可能性があります。そのため、よりランダム性の高い真の乱数の生成が求められています。
乱数の生成は元来、複雑な物理現象を数値的に研究するための方法として行われるようになったもので、現在では様々な科学分野のシミュレーションなどで極めて有用な道具になっています。しかし疑似乱数の場合には、その生成アルゴリズムに起因する乱数列の偏りが避けられないため、その実際的な影響の低減が課題となっており、この事情は暗号鍵の場合とも共通しています。
これらの課題に対応するためには、人為的なアルゴリズムの代わりに、ランダムとみなせる物理現象を利用する物理乱数が使われます。現在、主に使われている物理乱数は熱雑音による抵抗器の電圧変動といった複雑な物理現象を利用したものですが、今後の解析により知られざる規則性が発見され、ランダム性や秘匿性が失われる可能性があります。つまり、現在、主に使われている物理乱数もその生成過程の解明などで時間経過とともに安全性が相対的に低下していくという問題をかかえています。
この問題を最終的に解決すると期待されているのが量子乱数です。これは、物理乱数の中でも特に量子物理の原理的な確率性(非決定性)に基づいて生成されたものであり、そのために真の乱数としての望ましいランダム性を持ち、長期に渡って予測不可能な(秘匿性のある)ものと考えられています。
量子乱数を生成するには、単一光子から成る弱い光子ビームを発生させ、これをハーフミラー(半透明鏡)に通過させ、「透過」または「反射」の確率性を基に生成する方式が用いられています。しかし、これはビームを発生させるためのエネルギー源やハーフミラーを組み込むための一定の装置のサイズを必要とするという短所がありました。
これとは別の量子乱数生成法として、放射性原子から出る放射線の放出タイミングを乱数として取り出す方式も、従来から提案されてきました。この方式の長所は、放射性原子を小さなチップの中に埋め込むことが可能であり、光子ビーム方式のようなエネルギー源や装置サイズの問題が避けられることにあります。その一方、光子ビームの場合よりも複雑な核崩壊の現象に基づくため、生成した乱数のランダム性と秘匿性の考察が難しくなる短所があり、これまでにそれらの厳密な証明は与えられていませんでした。
【研究内容と成果】
本研究の成果は、アルファ崩壊のようなパリティ対称性を持つ核崩壊の場合には、これを用いて生成された量子乱数のランダム性と秘匿性の両方を同時に保証できることを理論的に証明したことにあります。
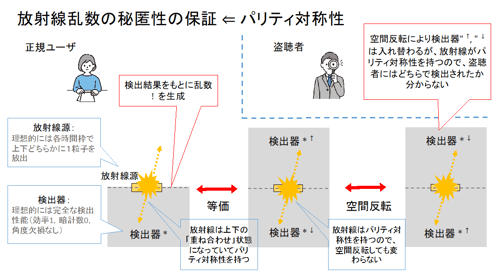
それが可能になった決め手は、「放射タイミングのランダム性」の利用を意図していた従来の方式の生データが、放射された粒子の「検出方向(上下)のランダム性」も含むということに着目したことです。この2重のランダム性のために、仮に前者の「放射タイミングのランダム性」が不完全であったとしても、後者の「検出方向(上下)のランダム性」がパリティ対称性によって原理的に保証されるため、全体としてのランダム性が確保されます。さらに、このパリティ対称性により、秘匿性も同時に保証されることが示されます。
やや詳しく言えば、アルファ崩壊は自然界の4つの基本的相互作用の中の「強い相互作用」と「電磁相互作用」の2種類の力が関与するものですが、この各々が空間反転に対するパリティ対称性を持つ相互作用であるために、アルファ崩壊の現象もパリティ対称性を持つことになります。このことは、崩壊したアルファ粒子が放射線源の上下のどちらにも一様にランダムに放出されることを保証します。つまり、自然界の相互作用の基本的性質が、生成された乱数のランダム性を保証するという構図です。
また、この方式で生成した乱数が外部の盗聴者に漏洩することがないことを保証するのも、このパリティ対称性です。なぜなら、もし仮に盗聴者が予め放射線源に何らかの細工を施して放射のタイミングの情報を一部知り得たとしても、放射線源にパリティ対称性がある限り、盗聴者が獲得できる情報は必ず空間反転の下で不変なものに限られるので、結果として上下どちらの検出器(これらは盗聴者が細工できません)で検出されたかの情報が得られなくなるからです。盗聴者が行う細工の一例としては、放射線源を含む正規ユーザの物理状態と盗聴者の状態とを予め関係づけておく(量子物理の用語では両者を「量子もつれ状態」にして相関を持たせておく)ことが挙げられます。しかし、パリティ対称性のために、測定結果を知る正規ユーザに直接関与できない盗聴者の状態には、検出器の上下の情報が消失していることが示されます。これにより、生成された乱数の秘匿性が保証されますが、これは再び、自然界の相互作用の基本的性質が、乱数の秘匿性を保証するという構図になっています。
【本研究の意義、今後への期待】
この研究で提案したパリティ対称性に基づく量子乱数生成が可能な核種として、アメリシウム(Am-241)を挙げることができます。アメリシウムは、既に一般家庭の煙式火災報知器等にも広く用いられていた放射線源ですが、乱数生成用としても、従来の「放射タイミングのランダム性」に基づく方式により、複数の企業により開発が進められ、既に数ミリ角のサイズのチップでの実装が低コストで可能になっており、実際に製品化もされています。本研究の結果、従来の方式における乱数抽出過程に最小限の変更を施すことで、真の意味で秘匿された乱数の生成が可能になります。これにより、今日の社会生活を支えている情報通信の機密性や金融決済での認証の信頼性を、より高いレベルに向上させることができます。将来的には、社会における情報の価値が一層、高まっていくことが予想されますが、その中には遺伝情報のような長期に渡って安全性が保たれるべきものも多くあると考えられます。本研究は、そのような長期に渡る安全性の要求に応えられる乱数源を単純な構造で実現する方法を与えるものです。
またこの研究は、量子力学における本質的な確率性と並んで、パリティ対称性という物理学の原理的な性質が理想的な量子乱数生成の実現に極めて重要な役割を果たすことを示すものであり、量子情報と素粒子・原子核物理分野の間に、新たな応用研究への連携の可能性を切り拓くものになっています。
【論文情報】
題目:Secure random number generation from parity symmetric radiations
著者:Toyohiro Tsurumaru, Toshihiko Sasaki, and Izumi Tsutsui
掲載誌:Communications Physics
DOI:10.1038/s42005-022-00915-1
【用語解説】
注1.ランダム性と秘匿性
暗号通信では、送信者が元の文(平文)を暗号化して受信者に送り、受信者は送信者から共有された暗号鍵を使って暗号文を複号して元の文を得る。その際、暗号文や暗号鍵に「特徴」があると解読される可能性があるため、数字の並びが完全にランダムな「真の乱数」にすることが求められる。加えて、乱数の生成過程において盗聴者が介入(細工)することも考えられるが、その場合は、ある程度、乱数が予測可能になって秘匿性が低くなる可能性がある。ランダムであっても秘匿性が低い場合があることに注意。
注2.パリティ対称性
自然界における空間座標の反転変換はパリティ(Parity)変換と呼ばれ、3次元空間の座標では(x,y,z)→(-x,-y,-z)の変換に対応する。これは物体を鏡に映す操作(と回転)に相当し、この変換の下で変化しない物体や現象はパリティ対称性を持つことになる。例えば原子核の放射性崩壊の場合、アルファ崩壊とガンマ崩壊はパリティ対称性を持ち、一方、ベータ崩壊はこの対称性を持たない。楊振寧と李政道はこの現象(ベータ崩壊でのパリティ対称性の破れ)を理論的に予想し、1957年のノーベル物理学賞を受賞している。
注3.暗号鍵
通信情報の暗号化やその復元(復号)といった暗号アルゴリズムを動作させるための「鍵」として使用されるデータ。現代暗号では暗号アルゴリズム自体は公開されるため、暗号鍵の漏洩や公開データからの解読が可能である場合は、暗号の安全性が失われる。
プレスリリース本文:PDFファイル
Communications Physics:https://www.nature.com/articles/s42005-022-00915-1
おすすめ記事
本件に関連する記事はこちら
対称性の下での量子擬似ランダム性の振る舞いを解明 ―より効率的な量子情報処理手法の開発に向けて―
網羅的なトポロジカル超伝導物質探索へ向けた新データベースの構築


