発表のポイント
◆ 物性物理学の量子シミュレーションに必要とされる計算リソースに関する解析・試算を行い、量子計算機が古典計算機(スーパーコンピュータ)を凌駕する「量子優位性」の最小条件を、世界で初めて明らかにした。◆ 量子化学や暗号解読といった分野に比べ、物性物理学への応用は、計算時間・量子ビット数の観点で1桁以上も少ないリソースで量子優位性を達成可能であることを示した。
◆ 本研究成果は、今後の量子計算機の研究開発に対して、中長期的な設計目標を示す役割を果たすものと期待される。また、本研究で用いられた解析手法・アルゴリズムは、材料科学・量子化学などの問題にも同様に応用可能であることから、理論的・基礎科学的なインパクトだけでなく、産業応用への知見も大きいものと期待される。

量子優位性を示すための要件:物性物理における量子シミュレーションは他の応用と比べて格段に
要求リソース(量子ビット数:計算機の規模、実行時間:答えを出すために必要な時間)が少ない。
概要
東京大学大学院工学系研究科物理工学専攻の吉岡信行助教、東京大学大学院理学系研究科量子ソフトウェア寄附講座の大久保毅特任准教授、日本電信電話株式会社コンピュータ&データサイエンス研究所の鈴木泰成准特別研究員、小泉勇樹インターン生(研究当時)、および大阪大学量子情報・量子生命研究センターの水上渉教授らによる研究グループは、量子誤り訂正(注1)機能を備えた量子計算機が、古典計算機を凌駕する、すなわち量子優位性(注2)を達成するための条件を明らかにしました。
計算量理論(注3)による定性的な解析によれば、量子ダイナミクスや暗号解読といった問題において、量子計算機は古典計算機よりも高速に問題を解くことができます。一方で、必要とされる計算時間や計算リソースがどの程度かという定量的な観点からは、現実的な範囲で達成可能な量子優位性があるのか、不透明な状況にありました。本研究では、最先端の古典・量子アルゴリズム(図1)を精緻に解析することで、物性物理学(注4)における量子優位性の達成に要求される計算リソースが、他の応用先と比べて格段に小さいことを示しました。本研究成果は、未来の量子計算機がめざすべきターゲットを提示しており、世界中の研究開発の指針となることが予想されます。また、本研究で用いられた解析手法は極めて一般的であることから、材料科学・高エネルギー物理・微分方程式の求解といった応用にも波及することが期待されます。

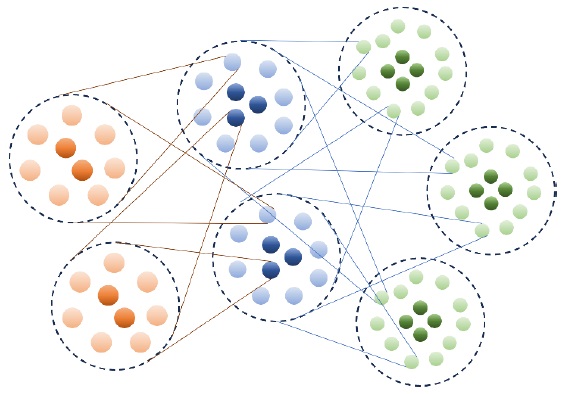
図1:量子位相推定アルゴリズムの模式図
量子ユニタリ操作𝑈の元で、興味の対象である量子状態|𝜓⟩が獲得する複素位相が、測定によって得られる。今回の研究では、物性物理学における基底状態のエネルギーを測定する量子アルゴリズムの設計や、実行時間・リソースの見積もりを行った。
発表内容
【研究背景】
量子計算機とは、状態の重ね合わせと干渉といった、量子力学の原理をうまく活用して計算を実行する計算機のことを指します。現在すでに実現している量子計算機は、ノイズの影響を強く受けてしまい、その計算精度は限られているものの、量子誤り訂正と呼ばれる機構によって計算精度を高めることができれば、量子化学や機械学習などにおいて、古典計算機よりも高速な計算が可能になる(量子優位性)と考えられています。しかし、これまでの研究は、計算量のオーダー解析(答えを出すために必要な演算の回数をおおまかに見積もること)に基づくものが主流で、実際の計算時間を知ることはできません。これまでに量子化学や暗号解読といった分野で、計算時間の定量的な解析が行われてきたものの、量子優位性の実現に必要な計算時間は丸一日以上と推定されていました。このような分野では、確かに量子計算機の方が古典計算機よりも早く答えを出せるものの、それでも答えが出るまでに時間がかかりすぎる、という問題を抱えていました。
【研究内容】
本研究では、新たに物性物理学と呼ばれる分野への応用に着目し、量子優位性の達成に必要とされる計算リソースが、これまでに知られていた応用例よりも格段に少ないことを示しました。具体的なターゲットは、物性物理学における代表的な難問として知られる、2次元の強相関量子多体模型における基底状態エネルギーの計算です。基底状態は、模型が取りうる量子状態の中で最もエネルギー的に安定な状態であり、量子相関・多体効果が最も強く創発する状態であることから、古典力学では相当するものがない、不可思議な現象が起こるものと考えられています。
量子優位性を議論する際には、古典・量子アルゴリズム(答えを求めるための手続き)のいずれに関しても、最速に動作するようなアルゴリズムの計算時間を見積もることが必要となります。本研究は、前者に関してはテンソルネットワーク法(注5)、後者に関しては量子位相推定法(注6)に関する計算時間の解析を行いました。特に、量子位相推定法は、ターゲットとする量子状態が、量子力学的な操作に対してどのような応答を返すかを調べるアルゴリズムですが、プローブの設計や量子状態の生成には膨大な選択肢があります。本研究では、これらを網羅的に調べることで最良の設計を特定したのち、10億を超える数の量子ゲートを書き下すことで、計算時間の緻密な解析を行いました。一方で、古典計算手法であるテンソルネットワーク法に関しては、実際にスーパーコンピュータ上で実行した計算結果に基づいて解析を行いました。
解析の結果、物性物理学における代表的な強相関量子多体模型においては、数十万の物理量子ビット(注7)によって数百の論理量子ビット(注8)を構成するような量子計算機を用いれば、数時間のスケールで量子優位性が発生することが明らかになりました(図2)。現代においてすでに、物理量子ビットを100個程度備えた量子計算機が実現しており、2030年代には10万単位の物理量子ビットを備えた量子計算機が実現するとの試算もあることから、本研究の提示する要件は中長期的なゴールとして達成可能なものと考えられます。

図2:物性物理学における代表的な量子多体模型における計算時間の見積もり
いずれの模型においても、論理量子ビットを100個程度活用する計算において量子優位性が発生している。本研究では、量子計算機の規模に応じて、量子アルゴリズムの「並列化」が可能であること、それにより大幅な高速化が見込まれることを明らかにした。また、古典計算機に関しても、CPUに基づくスーパーコンピュータではなく、GPUに基づく計算を実行すれば、数十倍程度の高速化が予想されるが、量子優位性の発生領域に大幅な変化はない。
【研究の意義、今後の展望】
本研究成果により、実用的な量子優位性達成に必要とされるハードウェアの仕様が明らかになりました。量子誤り訂正に関する小規模な実験が近年進展する中で、中長期的な未来にめざすべき到達点を示すことは、今後の誤り耐性量子計算機開発の指針としての役割を果たすため、量子技術の研究開発に対する重要な貢献と考えられます。また、今回の研究成果に触発されて、物性物理学に止まらず、材料科学・高エネルギー物理・微分方程式の求解といったさまざまな分野において、古典計算機によって到達可能なフロンティアを明らかにする試み、さらにそれを量子計算機で凌駕しようという試みが、さらに進展することが期待されます。
発表者・研究者等情報
東京大学
大学院工学系研究科 物理工学専攻
吉岡 信行 助教
小泉 勇樹 修士課程
研究当時:日本電信電話株式会社 コンピュータ&データサイエンス研究所 インターン生
大学院理学系研究科 量子ソフトウェア寄付講座/附属知の物理学研究センター
大久保 毅 特任准教授
日本電信電話株式会社 コンピュータ&データサイエンス研究所
鈴木 泰成 准特別研究員
大阪大学 量子情報・量子生命研究センター
水上 渉 教授
論文情報
雑誌名:npj Quantum Information
題 名:Hunting for quantum-classical crossover in condensed matter problems
著者名:Nobuyuki Yoshioka*, Tsuyoshi Okubo*, Yasunari Suzuki*, Yuki Koizumi, and Wataru Mizukami*
DOI:10.1038/s41534-024-00839-4
URL:https://www.nature.com/articles/s41534-024-00839-4
研究助成
本研究は、JST さきがけ研究(課題番号:JPMJPR1912、JPMJPR1916、JPMJPR191A、JPMJPR2119)、JST 共創の場形成支援プログラム(課題番号:JPMJPF2014、JPMJPF2221)、JST ムーンショット(課題番号:JPMJMS2061)、MEXT Q-LEAPフラグシップ(課題番号:JPMXS0120319794)、科研費(課題番号:22K18682、22H01179、23H03818)、IBM Quantumによる助成、東京大学大学院理学系研究科「量子ソフトウェア」寄付講座の支援、東京大学物性研究所による計算資源の助成により実施されました。
用語解説
(注1)量子誤り訂正
基本的な演算素子である量子ビットを多数組み合わせて情報に冗長性を持たせることで、ノイズによる計算の誤りに対して頑強に動作するような機構のこと。量子誤り訂正機能を備えた量子計算機を、誤り耐性量子計算機と呼ぶ。
(注2)量子優位性
量子計算機による計算時間が、古典計算機よりも短くなること。
(注3)計算量理論
解きたい問題の持つ数学的性質を抽出し、答えを出すために必要な計算時間の振る舞いをおおまかに調べる分野のこと。計算複雑性理論とも呼ばれる。
(注4)物性物理学
物質中の原子や電子の振る舞いを調べる学問のこと。凝縮系物理学とも呼ばれる。
(注5)テンソルネットワーク法
テンソル分解により情報圧縮された量子状態(テンソルネットワーク)を用いて量子系の振る舞いを調べる古典アルゴリズムのこと。
(注6)量子位相推定法
入力された量子状態を固有状態に持つようなユニタリ演算のもと、量子状態が獲得する固有位相を読み出すアルゴリズムのこと。入力が固有状態の重ね合わせである場合には、その重みに応じて確率的に固有位相が読み出される。
(注7)物理量子ビット
ハードウェア上にて実際に実装される量子ビットのこと。超伝導回路・中性原子・イオン・光学系による物理量子ビットなどが知られる。
(注8)論理量子ビット
物理量子ビットを多数組み合わせて、量子誤り耐性を獲得した量子ビットのこと。
プレスリリース本文:PDFファイル
npj Quantum Information:https://www.nature.com/articles/s41534-024-00839-4
おすすめ記事
本件に関連する記事はこちら
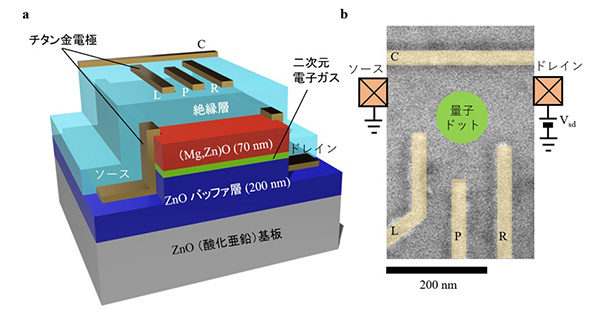
酸化亜鉛における電界制御量子ドット形成と量子多体効果観測を実現 ─新材料量子デバイス開発に期待─

高速でリアルタイムな光量子もつれ生成 ―従来の1000倍以上の高速量子相関が開拓する新時代―