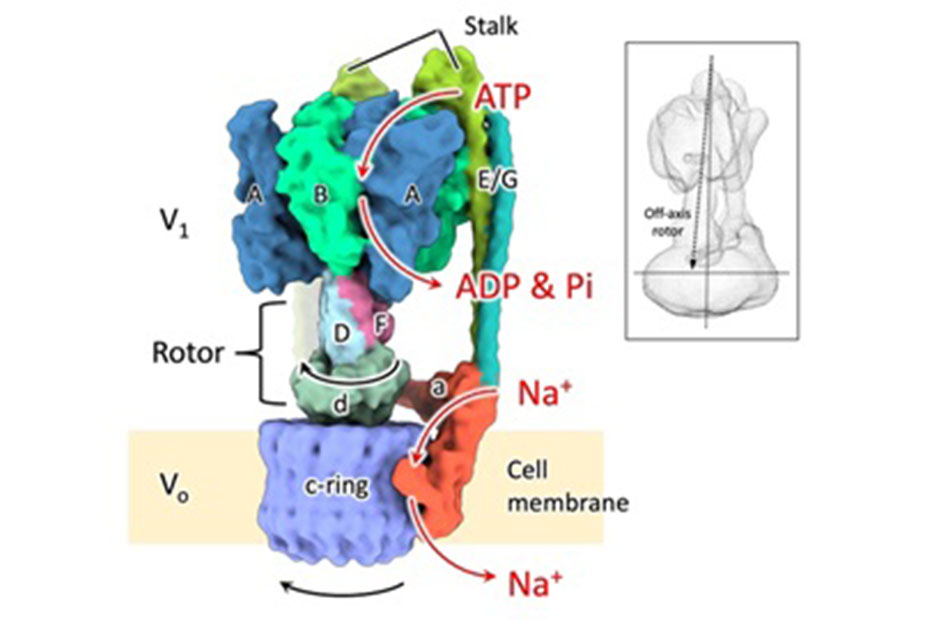
Share this
We have generalized the well-known statement that the Clifford group is a unitary 3-design into symmetric cases by extending the notion of unitary design. Concretely, we have proven that a symmetric Clifford group is a symmetric unitary 3-design if and only if the symmetry constraint is described by some Pauli subgroup. We have also found a complete and unique construction method of symmetric Clifford groups with simple quantum gates for Pauli symmetries. For the overall understanding, we have also considered physically relevant U(1) and SU(2) symmetry constraints, which cannot be described by a Pauli subgroup, and have proven that the symmetric Clifford group is a symmetric unitary 1-design but not a 2-design under those symmetries. Our findings are numerically verified by computing the frame potentials, which measure the difference in randomness between the uniform ensemble on the symmetric group of interest and the symmetric unitary group. This work will open a new perspective into quantum information processing, such as randomized benchmarking, and give a deep understanding to many-body systems, such as monitored random circuits.
PRX Quantum: https://journals.aps.org/prxquantum/abstract/10.1103/PRXQuantum.4.040331
These Related Stories