1.発表者:
乾 幸地(理化学研究所 量子コンピュータ研究センター 量子計算理論研究チーム 特別研究員)
求 幸年(東京大学 大学院工学系研究科物理工学専攻 教授)
2.発表のポイント:
◆ 欲しい物性から物質を探索する逆問題に対する新しい理論手法を開発しました。
◆ニューラルネットワークなどで用いられる自動微分を応用することで、人の手に頼らない自動的な物質設計を可能にしました。
◆経験や勘に基づく従来の物質設計を超えて、新物質や未知の指導原理を発見することが期待されます。
3.発表概要:
東京大学大学院工学系研究科物理工学専攻の乾幸地大学院研究生(研究当時)と求幸年教授は、目的の物性値が最適な値となる物質を見つける逆問題(注1)において、ニューラルネットワークで用いられる自動微分(注2)を応用することで、最適なモデルを自動的に設計する新しい理論手法を開発しました。機械学習の一つであるニューラルネットワークでは、与えられたデータを再現するように、大量の変数の最適化を自動微分と呼ばれるアルゴリズムの一種である誤差逆伝播法(注3)を用いて行います。この自動微分は、ニューラルネットワークに限らず幅広い計算に応用することが可能です。本手法では、注目する物性値が最適となるように、モデル中に仕込んだ大量の変数を自動微分を用いて最適化することによって新しいモデルを自動的に構築します。これを適用することで、巨大な量子異常ホール効果(注4)を示す新しいモデルや、太陽光によって大きな起電力が生じるモデルが自動的に得られることを実証しました。この新手法は、汎用性が高い上に広範な変数空間における自動探索が可能なため、経験や勘に基づく従来の物質設計の枠を超え、未知の物質や指導原理の発見に寄与することが期待されます。
本研究成果は、2023年3月1日(英国時間)に英国科学雑誌「Communications Physics」のオンライン版に掲載されました。また、本研究に関連した特許を出願中です。
本研究は、JSPS科研費 新学術領域研究「量子液晶の物性科学」(グラント番号:JP19H05825)、JSPS科研費(グラント番号:20H00122)、JST CREST(グラント番号:JPMJCR18T2)の支援を受けたものです。
4.発表内容:
物質科学の究極の目的は、望みの性質を示す物質や材料を自在に作り出すことです。実際に実験を行うことなく結果を予測する計算機シミュレーションは、この目的達成に向けた有効な方法の一つです。こうしたシミュレーションでは、これまでの研究の蓄積や研究者の経験・勘、あるいは第一原理計算(注5)などに基づいてモデルを構築し、モデル中の変数を変化させながら網羅的に調べることによって、最適な物質を探索することがしばしば行われます(図1)。しかし、変数の数が多くなると膨大な計算コストが必要となるため、ほとんどのシミュレーションは変数が少ないモデルに限定されてきました。そのため、このようなアプローチには、既存の枠組みを超える新しいモデルや物質を発見することが難しいという問題があります。この困難を克服するために、目的の性質から逆にモデルや物質を推定するという逆問題が注目を集めています。とりわけ、機械学習を用いたベイズ推定(注6)や生成モデル(注7)などを用いた研究が近年盛んに行われています。しかし、こうしたアプローチにも、大量の学習データや計算リソースが必要となることや、学習データの範囲を超えた推定は難しいといった問題点が残されていました。
このような問題点を解決するために、本研究では、任意の物理的な性質に対して、それを実現するモデルを自動的に構築する新しい手法(図1)を開発しました。具体的には、ニューラルネットワークなどにおいて用いられる自動微分というアルゴリズムが、大量の変数の最適化に極めて有効であり、かつニューラルネットワークに限らず幅広く応用可能であることに着目し、これを逆問題に適用することによって、目的の物性を示すようにモデル中の変数を自動的に最適化する新しい手法を開発しました。この手法では、網羅的な探索は必要ないため、変数の数を増やすことによる困難は大幅に低減されます。そのため、広範な変数空間の中から、これまでにないモデルや物質を発見することが可能となります。
この新手法を二つの具体例に適用することで、その有効性を実証しました。一つ目は、異常ホール効果(図2)の最大化です。まず、蜂の巣構造をもつモデルに適用することによって、自発的な量子異常ホール効果を示すことで有名なハルデインモデル(注8)が自動的に再発見されることを示しました。さらに、三角格子上のモデルに適用することで、ハルデインモデルの6倍という巨大な異常ホール効果を示す新しいモデルを発見することに成功しました。二つ目の例は、太陽光の照射によって発生する起電力の最大化です。ここでは、物質中を動き回る電子と局在したスピンが相互作用するモデルに本手法を適用することで、約700 A/m2の光電流を発生するモデルを自動的に発見することに成功しました(図3)。この値は、ゲルマニウム半導体やペロフスカイト材料であるBaTiO3、ワイル半金属として知られるTaAsなどと比べて、同等かより大きなものとなっています。
今回新たに提案した手法は、目的とする物性やそれを実現するためのモデルを任意に選ぶことが出来る高い汎用性を有しています。また、広範な変数空間の中を自動的に探索するため、経験や勘に基づく従来の物質設計では到達することが難しい新しいモデルや物質を発見することが可能です。今後は、カーボンニュートラルな社会の実現へ向けて、高い発電効率や熱電変換効率といった物性を示す新物質や、トポロジカル物質、スピントロニクスデバイス材料などの探索への応用が期待されます。自動設計によるアプローチは、コンピュータの性能の向上につれてさらに有用となることが予想されます。人類社会の発展に大きく貢献する物質や指導原理の発見につなげるべく、本手法をさらに発展させ、さまざまな対象に適用していきます。
5.発表雑誌:
雑誌名:「Communications Physics」(オンライン版:3月1日)
論文タイトル:Inverse Hamiltonian design by automatic differentiation
著者:Koji Inui* and Yukitoshi Motome
DOI番号:10.1038/s42005-023-01132-0
アブストラクトURL:https://www.nature.com/articles/s42005-023-01132-0
6.用語解説:
(注1)逆問題
入力から出力を求める順問題とは逆に、出力から入力を推定する問題。本研究の場合には、入力はモデルに対応し、出力は物性値に対応する。図1も参照のこと。
(注2)自動微分
複雑な関数の微分値を計算するアルゴリズム。複雑な関数の計算が、加減乗除などの基本演算や初等関数の組み合わせで構成されていることを利用して、各構成要素の演算に対する連鎖律を用いることで微分値を計算する。
(注3)誤差逆伝播法
ニューラルネットワークの学習アルゴリズムの一種。自動微分において、出力から入力の微分値を計算するリバースモードと呼ばれるアルゴリズムのこと。
(注4)量子異常ホール効果
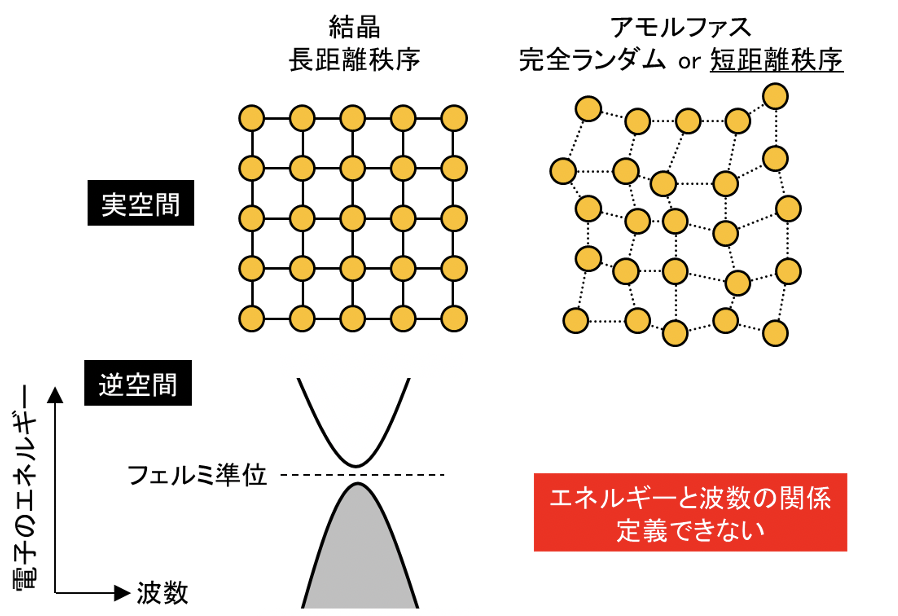
ホール効果とは、電流に対して垂直に磁場を印加することによって、電流と磁場の両方に垂直な方向に起電力が生じる現象。これに対し、異常ホール効果とは、強磁性体などで磁場が無い場合にも生じるホール効果を指す。量子異常ホール効果とは、異常ホール効果の中でもホール伝導度(電流に対する起電力の比)がある特定の値のみを示す現象。それに伴い、物質中を運動する電子のバンド構造がもつトポロジーに起因して、試料の端に散逸のない電流が生じる。図2も参照のこと。
(注5)第一原理計算
原子や分子、あるいは固体の構造や電子状態を、実験値や経験則に頼らずに、電子同士や電子と原子核の間のクーロン相互作用のみに基づいて計算する手法。
(注6)ベイズ推定
何も情報がない場合の予測を表す事前確率が、観測された新しいデータによってどう変化するのかを条件付き確率を用いて計算することによって、本当の確率を類推する手法。
(注7)生成モデル
機械学習において、大量の教師データからその特徴を学習することによって、教師データに似た新しいデータを生成出来るモデルのこと。近年では画像生成や機械翻訳に用いられている。
(注8)ハルデインモデル
1988年にF. D. M. Haldaneによって提案されたモデル。蜂の巣構造上で、隣り合う原子間とその次に近い原子間の電子の飛び移りのみを取り入れ、後者によって電子が有効的な磁場を感じると仮定することで、量子異常ホール効果が表れることを示した。この業績を含め、物質のトポロジカル相とそれらの間の相転移に関する理論的貢献に対して、F. D. M. Haldane他2名に2016年のノーベル物理学賞が与えられている。
7.添付資料:
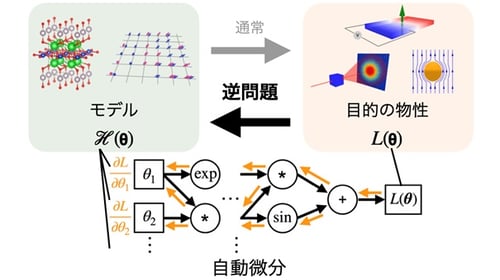
図1 目的とする物性からそれを実現するモデルを構築する逆問題における新手法の概念図。通常の理論計算では、仮定したモデルが含む変数を変化させながら物性値を網羅的に計算することで、目的となる物性を実現するモデルを探索します。これに対し、逆問題によるアプローチでは、まず目的の物性値を定めて、それが実現するようなモデルや物質を逆に求めます。今回開発した手法では、目的の物性値を表す関数Lを最適化するように、モデル中の変数θを自動微分を用いて最適化します。
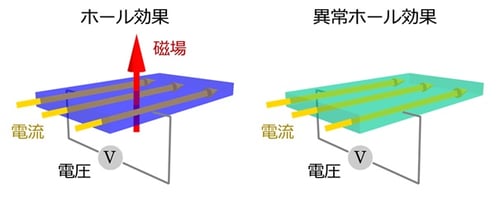
図2 ホール効果(左)と異常ホール効果(右)の概念図。磁場中に置かれた物質に電流を流すことによって、電流と磁場の両方と直交する方向に起電力が発生する現象をホール効果と呼びます。ある種の磁性体やトポロジカル物質では、磁場が存在しない場合でもホール効果が生じることがあり、これを異常ホール効果と呼びます。この異常ホール効果を最大化するように三角格子上のモデル中の変数を最適化したところ、自発的な量子異常ホール効果を示すことで知られているハルデイン模型の6倍の大きさの異常ホール効果を示すモデルを得ることに成功しました。
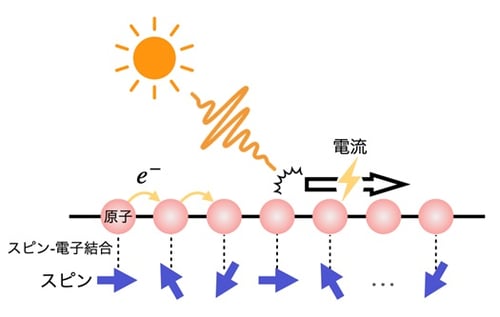
図3 動き回る電子と局在したスピンが結合した物質に太陽光照射することで電流が発生する概念図。この光起電流を最大化するようにモデル中の変数を最適化させたところ、半導体やトポロジカル物質に匹敵する約700 A/m2の光電流を生じるモデルを求めることに成功しました。
プレスリリース本文:PDFファイル
Communications Physics:https://www.nature.com/articles/s42005-023-01132-0
おすすめ記事
本件に関連する記事はこちら
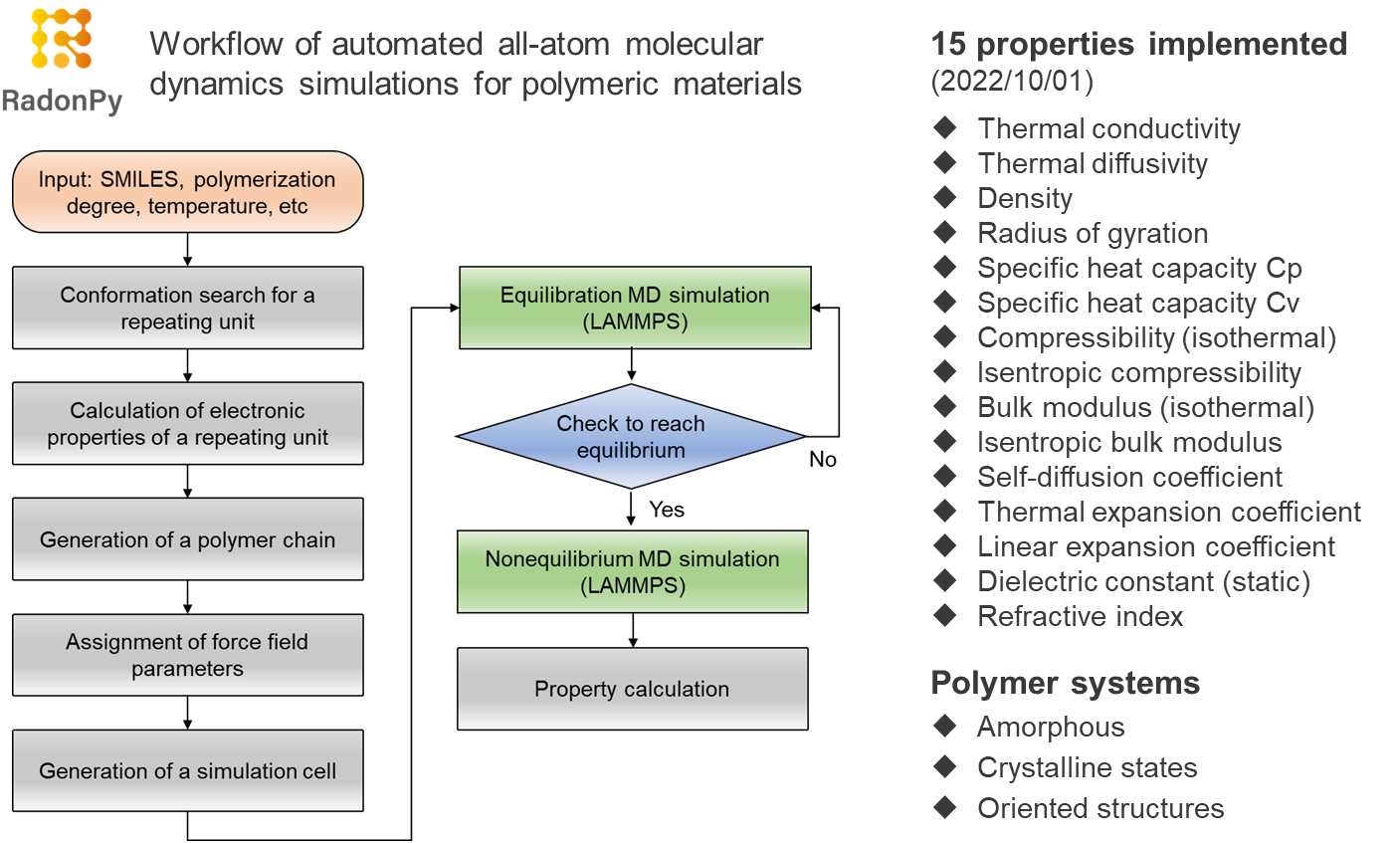
全原子古典分子動力学法による高分子物性計算を全自動化する ソフトウェアRadonPyをリリース ~高分子材料物性大地図の作成に向けた第一歩~
鉄シリコン化合物における新しいトポロジカル表面状態 -ありふれた元素を用いたスピントロニクス機能の実現-