発表のポイント
◆ 従来、磁石の中の磁気の振動は短い時間でなくなってしまうと考えられてきた。
◆ 本研究では、磁気振動を精密に読みだす手法を開発し、磁気振動の情報(コヒーレンス)が桁違いに長い間隠れて存在できる新たな情報保持機構を発見した。
◆ 今回の発見は、新たな磁気情報デバイスの原理になるものと期待できる。
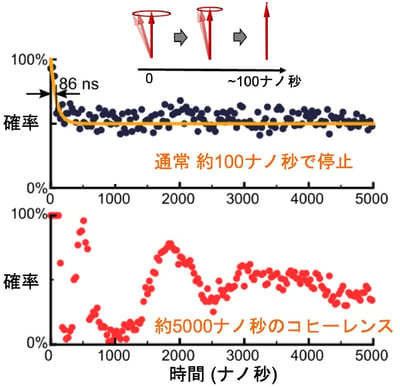
隠されていた磁気振動の情報(コヒーレンス)を取得
概要
東京大学大学院工学系研究科の巻内崇彦特任助教、日置友智助教、清水祐樹大学院生、星幸治郎特任研究員、齊藤英治教授(東北大学材料科学高等研究所(WPI-AIMR) 主任研究者、東京大学Beyond AI 研究推進機構 教授を兼務)らを中心とする研究グループは、東北大学材料科学高等研究所(WPI-AIMR)のMehrdad Elyasi助教、Gerrit Ernst-Wilhelm Bauer主任研究者らと共同で、従来、磁石の中で短い時間しか存在できないと考えられていた磁気振動の情報(コヒーレンス)が桁違いに長い時間隠れて存在できる機構を発見し、それを取り出せることを明らかにしました。
磁石の中のコヒーレンスは0と1両方の情報を扱える可能性がありますが、その状態を長く保つのが難しいため応用が困難と考えられていました。今回、磁石に隠されたコヒーレンスを取り出せたことで、磁気情報デバイス開発の道が拓けたと言えます。
本研究成果は、英国科学雑誌「Nature Materials」に2024年2月6日(英国時間)に掲載されました。
発表内容
〈背景と経緯〉
磁気の振動からはさまざまな情報を得ることができます。たとえば、磁気振動の速さは物質の種類や空間分布の情報を与えるため、元素分析や医療の現場で役立っています。磁石に外部から磁場を与えると、磁気振動状態を生成できます。スピンが揃って動く磁気振動には0や1の情報を対応させることができるため、この性質を情報デバイスなどに活用すれば常温で動作する演算素子を作ることが可能です。しかし、この磁気振動の情報(コヒーレンス)は短い時間で失われてしまうという、活用に向けての大きな問題がありました(図1)。もし、より長い時間が経ってからでもコヒーレンスの情報を取り出せるとしたら、室温動作する磁気情報デバイスへの応用が期待できます。そこで本研究では、コヒーレンスを測る新しい実験手法を開発し、コヒーレンスが存在できる機構の実証に挑みました。
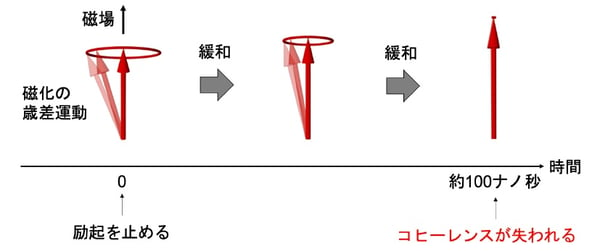
図1:通常の磁化歳差運動
物質の中にはスピン(ミクロな磁石)がたくさん存在し、磁石では電子のスピンの向きが揃って磁化(図中の赤矢印)を形成する。物質に磁場をかけると、磁化は磁場の周りを振動(歳差運動)する。マイクロ波による励起中はスピンが揃って動くためコヒーレンスを保った歳差運動が続くが、励起を止めると、スピンが摩擦で止まり始め、約100ナノ秒後にはコヒーレンスは失われると考えられてきた。
〈研究内容〉
磁石(強磁性体)の中には多数の電子スピンが磁場の方向に揃った状態(磁化)で存在しています。これに外部からマイクロ波の振動磁場を与えると、電子スピンは力を受け、一斉に磁場の周りを振動します(歳差運動・図1)。この振動のコヒーレンスは外部からマイクロ波を与え続ける限り維持されますが、マイクロ波を止めると摩擦によって減衰するためコヒーレンスが失われていきます。
本研究では、外部からの力を絶った後の磁気振動の情報を取り出す測定法(ポンプ-プローブ測定)を開発しました(図2)。この測定方法は、パラメトリック励起というブランコの立ちこぎと同じ原理を用います。ブランコの立ちこぎでは、身体を上下に動かすとブランコを大きく動かすことができます。それと同じように、共鳴周波数(パラメーター)を周期的に変化させ、その半分の周波数の振動を引き起こすのがパラメトリック励起です。ここで重要なポイントは、励起を開始した瞬間にブランコが前に進むか(0位相)後ろに進むか(π位相)という点です。例えば0位相が実現する確率のほうが大きかった場合、ブランコが0位相のコヒーレンスを持っていたことがわかります。
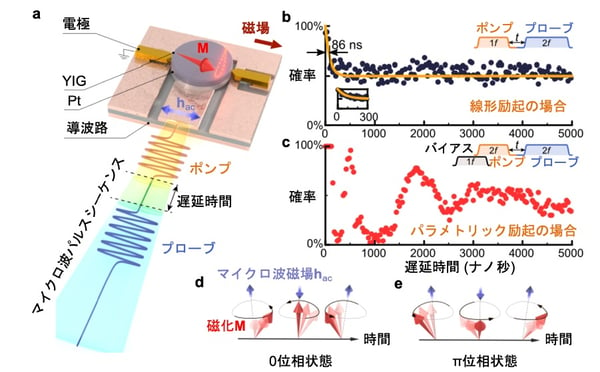
図2:測定方法の概念図と結果
(a)ポンプ–プローブ測定の模式図。イットリウム鉄ガーネット(YIG)と白金(Pt)を積層した微小円盤を導波路の上に載せマイクロ波パルスを印加することで、磁化の歳差運動を励起する。パルスシーケンスはポンプパルス印加、何も印加しない遅延時間、プローブパルス印加の順番になっている。(b)ポンプが線形励起の場合の結果。縦軸は最初に作った歳差運動と同じ0位相状態がプローブで実現された確率。遅延時間がゼロだと100%の確率で0位相状態が読み出されたが、約100ナノ秒後には50%(つまりランダム)になった。(c)パラメトリック励起のポンプパルスを印加した結果。遅延時間が5000ナノ秒まで50%に落ち着かず何度も振動していることは、隠れたコヒーレンスが存在していることを示唆する。(d)0位相状態の模式図。(e)π位相状態の模式図。
この測定法を何度も繰り返し、磁石のコヒーレンスがどれだけ長く存在できるかを調べました。最初に共鳴周波数と同じ周波数の力を加えた場合では、予想通り、約100ナノ秒後にはコヒーレンスが失われ、0位相を読み出す確率が50%(コイントスと同様なランダムさ)になりました。一方、最初にパラメトリック励起を行うと、約5000ナノ秒という桁違いに長い時間まで何度も振動することがわかりました。もちろん通常の意味における磁化の歳差運動は約100ナノ秒で失われるので、この結果はコヒーレンスが約5000ナノ秒“隠れて”存在していたことを示唆しています。
この確率振動を説明するため、研究グループはさらに理論モデルを構築し、検証実験を行いました(図3)。理論モデルでは、コヒーレンスの情報を半分の周波数の運動に埋め込み、その情報を再び元の周波数として取り出す機構を考案しました。実験では、磁化歳差運動の振幅・位相・ゆらぎを取得する状態トモグラフィ(注1)を利用して振幅の時間変化を測定し、理論と同じ特徴的な2つの傾きが現れることを実際に観測しました。以上の結果から、桁違いに長い時間磁気振動の情報を保持できる機構が存在し、その隠されていた情報を取り出せることが明らかになりました。
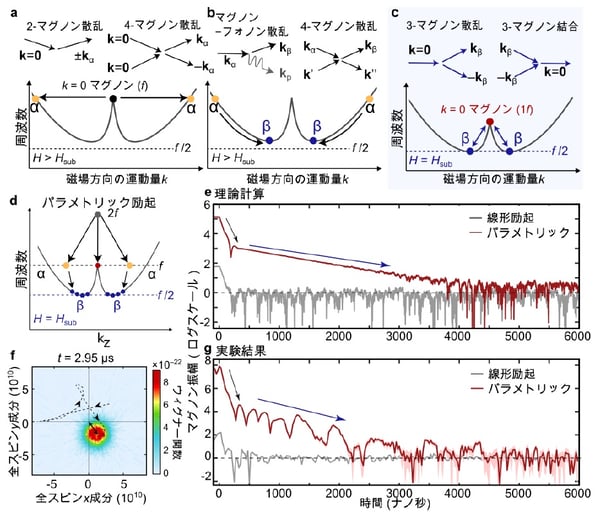
図3:理論モデルの概念図と実験結果
(a–d)スピン波を量子化したマグノンの周波数–運動量の関係(分散関係)。底に蓄積したマグノンに隠れたコヒーレンスが存在し、3-マグノン結合(注3)とパラメトリック励起でそのコヒーレンスを取り出す過程を表している。(e)理論モデルに基づく数値計算で得たマグノン振幅の時間変化。(f)状態トモグラフィ測定によって得たマグノンのウィグナー関数の軌跡。(g)状態トモグラフィ測定で得たマグノン振幅の時間変化。
〈研究の学術的・工学的意義と今後の展望〉
今回、磁石に隠されていた磁気振動を発見し、その情報を取り出せたことで、磁気情報デバイス開発への可能性を拓いたと言えます。今回発見した情報保持機構は、スピントロニクスや磁性の分野だけでなく、材料物理学・物性物理学の広範囲に影響を与えるものと考えられます。また、磁性体をナノメートルサイズに集積化し演算素子やメモリに利用する際も、この原理により隠れたコヒーレンスを利用できるようになります。今後は磁石の物理がさまざまな量子物性物理学の領域と融合するように展開していくと期待できます。
発表者・研究者等情報
東京大学大学院工学系研究科
巻内 崇彦 特任助教
日置 友智 助教
清水 祐樹 博士課程
星 幸治郎 特任研究員
齊藤 英治 教授
兼:東北大学材料科学高等研究所(WPI-AIMR) 主任研究者
兼:東京大学Beyond AI 研究推進機構 教授
東北大学材料科学高等研究所(WPI-AIMR)
Mehrdad Elyasi 助教
Gerrit Ernst-Wilhelm Bauer 主任研究者
論文情報
雑誌名:Nature Materials
題 名:Persistent magnetic coherence in magnets
著者名:T. Makiuchi*, T. Hioki*, H. Shimizu*, K. Hoshi, M. Elyasi, K. Yamamoto, N. Yokoi, A. A. Serga, B. Hillebrands,
G. E. W. Bauer and E. Saitoh (*Equal contribution)
DOI:10.1038/s41563-024-01798-z
URL:https://www.nature.com/articles/s41563-024-01798-z
研究助成
本研究は、科学技術振興機構(JST)戦略的創造研究推進事業CREST 非古典スピン集積システム(No.JPMJCR20C1)、戦略的創造研究推進事業ERATO 齊藤スピン量子整流プロジェクト(No. JPMJER1402)、日本学術振興会(JSPS)科学研究費助成事業(No.JP26103005、JP19H00645、JP19H05600、JP20K15160、JP21K13847、JP21K13886、JP22K14584、JP22H04965、JP22H05114)、東京大学・ソフトバンクBeyond AI連携事業などによる支援を受けて行われました。
用語解説
(注1)状態トモグラフィ
状態トモグラフィとは、対象とする物理系の射影測定により物理状態を特徴づける確率分布関数(ウィグナー関数)を同定する実験方法である。ウィグナー関数は位置と運動量のように正準共役な関係(注2)にある力学変数の関数であり、分布の平均値は振幅と位相を、広がりはゆらぎを表す。
(注2)正準共役な関係
正準共役な関係とは、2つの量が互いに相関し合い、明確に区別できない関係である。量子力学において正準共役な関係にある2つの物理量の値は同時に測定することができず(不確定性原理)、一定の誤差でゆらいで観測される。
(注3)3-マグノン結合
3-マグノン結合とは、2つのマグノンが結合して1つのマグノンになる過程のこと。周波数(エネルギー)と運動量は保存される。その他、その逆過程も含めた3-マグノン散乱、マグノンが磁石の表面などで散乱される2-マグノン散乱、2つのマグノンが衝突して別の周波数・運動量に散乱する4マグノン散乱、マグノンが音波を量子化したフォノンを吸収・放出するマグノン-フォノン散乱などがある。
プレスリリース本文:PDFファイル
Nature Materials:https://www.nature.com/articles/s41563-024-01798-z
おすすめ記事
本件に関連する記事はこちら
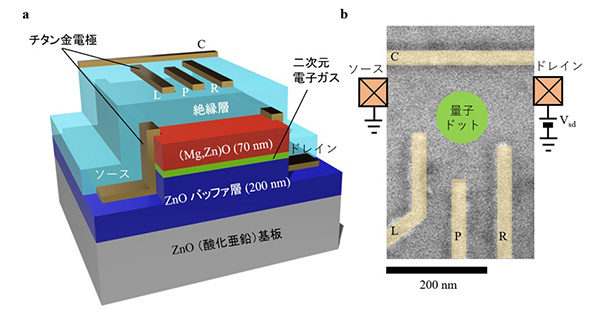
酸化亜鉛における電界制御量子ドット形成と量子多体効果観測を実現 ─新材料量子デバイス開発に期待─

セラミックスにおける新拡散メカニズムを発見 ―セラミックスの焼結メカニズムの解明と新たな粒界設計指針の構築―