1.発表者:
Zhiqiang Liao(東京大学 大学院工学系研究科電気系工学専攻 博士課程2年)
Kaijie Ma(東京大学 大学院工学系研究科バイオエンジニアリング専攻 特任研究員)
Md Shamim Sarker(東京大学 大学院工学系研究科電気系工学専攻 博士課程2年)
Siyi Tang(東京大学 大学院工学系研究科電気系工学専攻 修士課程2年)
山原弘靖(東京大学 大学院工学系研究科電気系工学専攻 助教)
関 宗俊(東京大学 大学院工学系研究科附属スピントロニクス学術連携研究教育センター准教授)
田畑 仁(東京大学 大学院工学系研究科バイオエンジニアリング専攻/
電気系工学専攻 教授、Beyond AI研究推進機構)
2.発表のポイント:
◆我々の身の回りには、熱ゆらぎに代表されるノイズ(雑音)が満ち溢れています。コンピュータの動作においては、ノイズ(雑音)は誤動作、エラーの原因になるため、通常は厄介者として嫌われており、膨大な電力を消費してエアコンをフル稼働させてコンピュータを冷却して可能な限りノイズを小さくする努力がなされています。本研究では、この通常厄介者として嫌われているノイズが、使い方によっては大変役に立つことを発見しました。
◆ノイズは様々な種類が存在し、その特徴から“色”名称を付してレッドノイズ(赤色雑音)、ピンクノイズなどと呼ばれ、総称としてカラードノイズ(有色雑音)(注1)と呼ばれています。ゲイン散逸イジングマシン(注2)が組合せ最適化問題(注3)を解く過程において、カラードノイズを積極的に導入し、計算性能にノイズが及ぼす影響を詳細に検証しました。
◆レッドノイズをゲイン散逸イジングマシンに入力することでスピン状態変化のランダムエラーが抑制されるとともに、確率共鳴現象(注4)により最適解(エネルギー最小状態)を得る確率(正答率)が飛躍的に向上することを見出しました。環境に存在するカラードノイズの効果的利用によるイジングマシンの性能向上が初めて実証され、今後の環境援用超低消費エネルギー計算機への応用が期待されます。
3.発表概要:
東京大学大学院工学系研究科の山原弘靖助教、関宗俊准教授、田畑仁教授のグループは、イジングマシンに入力するノイズ分散を変調することにより、組合せ最適化問題の解決に確率共鳴現象を誘起し、性能向上に寄与することを初めて見出しました。従来の研究ではゲイン散逸イジングマシンの最適解(エネルギー最小状態)への発展において、ガウシアンホワイトノイズでは確率共鳴を誘起できないことが証明されており、ノイズ(雑音)を有効活用することができませんでした。したがって、従来の構成ではノイズを減らすか、システムの信号強度を増幅する必要がありました。本研究では、レッドノイズ(パワースペクトル密度が1/f 2に比例)をイジングマシンに入力することでスピン状態変化のランダムエラー発生頻度が減少することが明らかとなりました。さらにレッドノイズは確率共鳴を誘起することで、組合せ最適化問題を解く際にノイズが大きい条件下においても最適解を効率的に見つけることができました。本研究は従来、厄介者として考えられてきたノイズを効果的に利用することにより、組合せ最適化問題を解くイジングマシンの性能向上を提案するものであり、環境援用超低消費エネルギー計算機への応用が期待されます。
4.発表内容:
組合せ最適化問題は従来のコンピュータではNP困難(注5)として扱われ、社会経済、医学医薬から情報通信、物流、金融に至る多くの分野で重要な課題となっています。一方、これらの問題を解くために使用される現代のコンピュータ技術の発展を支えるムーアの法則には限界が迫っており、これまでのようにコンピュータ性能の指数関数的な性能成長は困難となっています。そこで組合せ最適化問題を解くために物理現象に基づく新しいコンピュータ概念の開発が活発に行われています。特に組合せ最適化問題を理論モデルにおけるスピン(注6)間の相互作用に変換し、最適解(エネルギー最小値)を探索する方法が期待されています。この方法では、光学系、電気機械系、電子回路、スピントロニクスなどさまざまな技術を用いてイジングマシンが実現されており、すでに数千個のスピンから構成されるイジングモデルの最適解計算は可能になっています。イジングマシンが真の最適解にたどり着くために、ノイズは局所解を抜け出すために使用されます。しかし、従来はガウシアンホワイトノイズが用いられ、ノイズが小さい状況でしかゲイン散逸イジングマシンは正常に動作しませんでした。ホワイトノイズの信号強度が大きくなると、スピン状態の変化にランダムエラーが発生し、組合せ最適化問題の最適解の正答率が低下します。もし、イジングマシンが大きいノイズに適応し、さらに組合せ最適化問題の正答率を向上させるノイズ変調の手法を発見することができれば、低消費電力で動作する強力なイジングマシンの実装が可能となります。そこで、我々は図1のようなパワースペクトル密度を示すカラードノイズに注目しました。様々なカラードノイズをゲイン散逸イジングマシンに入力し、最適解へのイジングハミルトニアンの発展を最も促進するノイズを発見しました(図2(a))。
本研究では、10×10=100個のスピンが強磁性的に結合した正方格子(注7)を用いて、様々なカラードノイズの存在下でイジングマシンのドメインクラスタリングのダイナミクスを調べました。その結果、ブルーやバイオレットノイズがイジングマシンに及ぼす影響はホワイトノイズと同様でした。一方、ピンク、レッドノイズによって最適解を求める計算速度はホワイトノイズと比べてそれぞれ3倍、8倍に加速化し、調査したカラードノイズの中ではレッドノイズが最も優れた効果を示しました。次に組合せ最適化問題の代表として、100個のスピンからなるMAXCUT問題(注8)を解きました。一般的には、単純なMAXCUT問題に対してノイズの増加は正答率を低下させます。しかし、メビウスラダーに対して、他のカラードノイズでは動作できないほどノイズが大きい場合でも、レッドノイズは60%の正答率を保ちました(図2(b))。より難しいMAXCUT問題(ランダム正方格子、ランダムメビウスラダー、図2(c,d))に対しても、ホワイト、ブルー、バイオレットノイズはイジングマシンの性能をノイズの増加とともに低下させます。さらにホワイト、ブルー、バイオレットノイズの入力したイジングマシンは60%以上の正答率を達成することができませんでした。一方、レッドノイズの入力の場合、最も高い80%の正答率を達成しました。さらに、レッドノイズは先行研究で報告の無い確率共鳴現象を誘起することも明らかとなりました。この結果は環境に存在するレッドノイズを利用することで、より優れた性能のイジングマシンが得られることを示しています。
以上の研究成果に基づき、我々はレッドノイズで駆動するイジングマシンの実装に取り組んでいます。電子のブラウン運動によってレッドノイズを発生させることができるため、スピントロニクスデバイスとFPGAの組合せにより高周波、低消費電力で動作するプログラム制御可能なイジングマシンの実現が期待されます。さらに自然界には多くの媒体でカラードノイズが存在し、光学系、電気機械系、電子回路、スピントロニクスなどさまざまな系でゲイン散逸イジングマシンが実現されることが期待されます。したがって、本研究成果はイジングマシンのダイナミクスの理解を深めるだけでなく、組合せ最適化問題を解くための専門的なソフトウェア設計に役立つと考えられます。ノイズ分散が新しいハイパーパラメータと成り得ることが示され、より柔軟に高速かつ効率的な新しいヒューリスティックアルゴリズムを実現することが期待されます。
5.発表雑誌:
雑誌名:「Advanced Theory and Simulations」(Wiley出版)
論文タイトル:Quantum Analog Annealing of Gain-dissipative Ising Machine Driven by Colored Gaussian Noise
著者:Zhiqiang Liao, Kaijie Ma, Md Shamim Sarker, Siyi Tang, Hiroyasu Yamahara*, Munetoshi Seki, Hitoshi Tabata
DOI番号:10.1002/adts.202100497
アブストラクトURL:https://doi.org/10.1002/adts.202100497
本論文は、イギリス時間1月11日(火)にオンライン掲載されました。
3月発行予定の冊子版の表紙に本論文が選出されました。
6.用語解説:
(注1)カラードノイズ(有色雑音):パワースペクトル密度が周波数fに対して1/fβとして定義されるものはべき乗則ノイズと呼ばれ、βの値により様々な色の名前が付けられている。β = -2, -1, 0, 1, 2のとき、それぞれパープル、ブルー、ホワイト、ピンク、レッドノイズと呼ばれている。特にβ = 1の場合が一般に知られている1/fノイズに相当する。
(注2)ゲイン散逸イジングマシン:イジングマシンは磁性体モデルの一つで、上向き、下向き2種類の極小磁石(スピン)の組み合わせで構成されていると単純化して取り扱うイジングモデルを基とし、最適化問題を高速に解くことに特化した計算機。ゲイン散逸イジングマシンはその一種で、系の双安定な非線形性と線形利得との相互作用によって、2値のスピン状態をシミュレーションする。
(注3)組み合わせ最適化問題:セールスマンが都市を一度ずつ訪問する最も効率の良い巡回路を求める「巡回セールスマン問題」や、ナップサックに食料や道具等の品物を詰める際、ナップサックの容量の範囲内でできるだけ有用な品物を選ぶ「ナップサック問題」など、与えられた条件の下で最も効率の高い解を導き出す問題として「組み合わせ最適化問題」と呼ばれている。
(注4)確率共鳴:信号にノイズ(雑音)を入力することにより、システムの応答が向上する現象。 生物の感覚器官による微弱信号検出や氷河期の周期などの自然現象を説明するモデルとして知られている。
(注5)NP困難:NP(Non-deterministic Polynomial time:非決定的多項式時間)に属する問題とは、証拠が与えられれば現実的な時間(多項式時間)で解く事の出来るが、証拠がなければ解けない問題を指し、NP困難とはこのNP問題と同等かそれより難しい問題を指す。NP困難な組合せ最適化問題は、一般に最適解を求めるアルゴリズムが計算完了までに指数関数時間を必要とするなどして、非常に困難であると考えられている。
(注6)スピン:量子力学上の概念で、粒子が持つ固有の角運動量であり、「仮想的な自転自由度」に由来する。本研究では+1または−1の2値の値をとる変数として扱う。
(注7)強磁性的に結合した正方格子:数学的における2次元ユークリッド空間の正方格子。全てのエッジにおける結合が強磁性的であれば、基底状態で全てのスピンが同じ方向に配向することが求められる。このスピン発展のプロセスがドメインクラスタリングと呼ばれている。
(注8)MAXCUT問題:複数のノード(点)とノードを結ぶエッジ(線)からなるグラフにおいて、ノード群を2つの部分集合に分割する際、異なるグループに属するノード間に貼られたエッジの数が最大となる分け方を求める問題。イジングモデルの最適解(エネルギー最小状態)を求める問題と一対一対応する。本研究では3つのMAXCUT問題(メビウスラダー、ランダム正方格子、ランダムメビウスラダー、図2(b-d))を対象とした。メビウスラダーでは頂点の数が4の倍数であるとき、近接スピン間の相互作用は反強磁性的になりフラストレーションが生じる。ランダム正方格子ではエッジの相互作用は強磁性的(Jmn = +1)あるいは反強磁性的(Jmn = −1)からランダムに選ばれる。このランダムな選択によって各エッジでフラストレーションが生じる。ランダムメビウスラダーはメビウスラダーとランダム正方格子の両方のフラストレーション特性を備えたトポロジーである。トポロジーの大きさが100個のスピンのとき、メビウスラダーは単純な問題だが、ランダム正方格子とランダムメビウスラダーは難しい問題となる。
7.添付資料: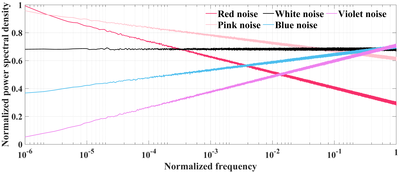
図1. 各カラードノイズ(レッド、ピンク、ホワイト、ブルー、バイオレットノイズ)のパワースペクトル密度。縦軸:各種のノイズ(雑音)の 単位周波数帯域幅あたりのパワースペクトル密度。横軸:規格化した周波数。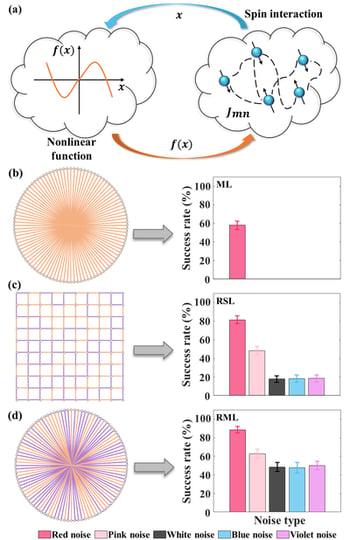
図2. (a) ゲイン散逸イジングマシンの概要図。xはフィードバックシグナル、非線形関数f(x)はスピン振幅(spin amplitude)を示し、m番目とn番目のスピンは重みJmnで相互作用している。フィードバックループで最適解を反復計算する。反復計算において、スピンの状態はf(x)の符号(スピンアップは正、スピンダウンは負)によって得られる。(b)メビウスラダー(Möbiums ladder : ML, ノイズの大きさD = 1)、(c)ランダム正方格子(random square lattice : RSL, D = 0.01)、(d)ランダムメビウスラダー(random Möbiums ladder : RML, D = 0.1)を各カラードノイズの入力下で500回反復計算した正答率。いずれの場合もレッドノイズの入力によって正答率が上昇した一方、ブルーノイズ、パープルノイズの入力では正答率はホワイトノイズと同等であった。ランダム正方格子とランダムメビウスラダーにおいてスピンはフラストレートしており、局所的なエネルギー最小値(局所解)が存在するため、従来のモンテカルロ法やホップフィールドネットワークでは最適解を発見することが難しい。人工スピンにおいて、強磁性的(Jmn = +1)、反強磁性的(Jmn = −1)相互作用を表すエッジをそれぞれ紫線、オレンジ線、頂点を白点で表している。
プレスリリース本文:PDFファイル
Advanced Theory and Simulations:https://onlinelibrary.wiley.com/doi/10.1002/adts.202100497
おすすめ記事
本件に関連する記事はこちら

