1.発表者:
三橋 洋亮 (東京大学 大学院工学系研究科物理工学専攻 博士課程2年)
金子 和哉 (研究当時:東京大学 大学院工学系研究科物理工学専攻 博士課程3年)
沙川 貴大 (東京大学 大学院工学系研究科物理工学専攻/附属量子相エレクトロニクス研究センター 教授)
2.発表のポイント:
◆量子力学特有の状況にも適用できる「対称性に保護された熱平衡状態」の概念を確立した。
◆本研究は、対称性を活用したより柔軟な量子熱機関の設計原理に繋がると期待される。
3.発表概要:
近年の量子制御技術の発展に伴い、新たな量子デバイスの創出に向けた理論的研究はより一層重要性を増しています。量子デバイスのエネルギー的な性質を解明することを一つの目標として、量子熱力学の研究が盛んに行われています。一方で、物理学ではさまざまな局面で対称性が現れますが、対称性の概念を導入することで量子熱力学がどのように拡張されるかは、重要な未開拓の問題でした。
東京大学大学院工学系研究科物理工学専攻の三橋洋亮大学院生、金子和哉大学院生(研究当時)、沙川貴大教授らは「熱平衡状態からの仕事の取り出しは不可能である」という熱力学第二法則(注3)に基づいて、対称性を持つ物理系における熱平衡状態のありうる形を全て同定し、それを数学的に厳密に証明しました。対称性の下では仕事の取り出しはより困難になり、より多くの状態が熱平衡状態として振る舞うようになりますが、そのような状態は「対称性に保護された熱平衡状態」と呼ぶことができます。
本研究結果は量子力学特有の状況にも適用でき、対称性を持つ物理系を用いたより柔軟な量子熱機関の設計原理に繋がると期待されます。
本研究成果は、2022年4月18日(米国東部夏時間)に科学雑誌「Physical Review X」のオンライン版に掲載されました。
4.発表内容:
【研究背景】
近年、量子系の制御技術の急速な発展に伴って、多彩な量子デバイスが実現されつつあります。そこで、そのような量子デバイスのエネルギー効率などの熱力学的性質を考察することを一つの目的として、ミクロな系における熱力学の研究が盛んに行われています。そのためには、原子・分子レベルのミクロ系についての理論である量子力学と、日常的なマクロ系についての理論である熱力学を統合する必要があります。対象とする物理系のスケールが異なるため、これら二つの学問分野を繋げるには多くの困難がありますが、それを乗り越えるべくさまざまな試みがなされています。
熱力学第二法則の一つの表現として、熱平衡状態からは如何なるサイクル操作によっても仕事を取り出せないというケルビンの原理があります。ケルビンの原理は量子熱力学においても成り立ち、それに基づいて熱平衡状態の量子力学的な特徴付けを得ることができます。しかし、対称性の下で許された操作だけを考えた時に、どのような状態が熱平衡状態として振る舞うかについては明らかにされていませんでした。
【研究内容】
本研究グループは、量子熱力学におけるケルビンの原理に基づいて、対称性の下での熱平衡状態のありうる形を全て同定しました。それらの状態は、対称性が無ければ熱平衡状態とは見なせなくなるため、「対称性に保護された熱平衡状態」と呼ぶことができます。具体的には、対称性の下で仕事を取り出すことができない状態は全て一般化ギブス分布(注4)になることを、量子力学に基づいて証明しました(図1)。ここで重要なことは、この結果は対称性によって保存される物理量が量子力学特有の非可換性(注5)を持つ場合、例えば、スピン(注6)が保存される場合にも成立するということです。このような場合の一般化ギブス分布については、これまであまり研究がなされておらず、本研究は量子熱力学の新しい概念を開拓したと言えます。
数学的な証明は、状態が一般化ギブス分布であれば対称性を満たすサイクル操作によって仕事を取り出せないことと、逆に仕事を取り出せないならば一般化ギブス分布であることの、二つの部分からなります。前半の証明は簡単にできる一方で、後半の証明をすることは数学的な難度が極めて高く、それが本研究の本質的な成果です。それを証明するために、一般化ギブス分布以外の任意の状態に対しては、対称性の下でも必ず仕事が取り出せることを、具体的なプロトコルを構成することで示しました。
【研究の意義、今後の展望】
本研究結果は、対称性の下では従来よりも多くの状態が熱的に安定であることを示唆します。本研究において明らかにした熱平衡状態の概念は、対称性の下での量子熱力学の根幹をなすものであり、今後の研究を展開していく上での基盤となると考えられます。さらに、対称性の下ではより多彩な状態を熱的に安定な状態として活用できるようになるため、より柔軟な量子熱機関の設計原理に繋がると期待されます。
【謝辞】
本研究は、東京大学統合物質・情報国際卓越大学院(MERIT-WINGS)、科学研究費補助金基盤研究(A)「孤立量子多体系における熱力学第二法則」(科研費番号JP16H02211)、科学研究費補助金新学術領域(研究領域提案型)「情報物理学でひもとく生命の秩序と設計原理」 の計画研究班「情報熱力学による生体情報処理の理論研究」(科研費番号JP19H05796)、および東京大学Beyond AI研究推進機構からの助成を受けて行われました。
5.発表雑誌:
雑誌名:「Physical Review X」(オンライン版:4月18日)
論文タイトル:Characterizing Symmetry-Protected Thermal Equilibrium by Work Extraction
著者:Yosuke Mitsuhashi*, Kazuya Kaneko, and Takahiro Sagawa
DOI番号:10.1103/PhysRevX.12.021013
アブストラクトURL:https://link.aps.org/doi/10.1103/PhysRevX.12.021013
6.用語解説:
(注1)熱平衡状態
熱いコーヒーが次第に冷めていき、十分時間が経つと室温と同じ温度になるように、物理系は十分長い時間が経過するとある状態に落ち着いていきます。このように定常で流れのない状態のことを熱平衡状態と言います。熱平衡状態を量子力学に基づいてどう理解すべきかは未解明で、現在も盛んに研究が行われています。
(注2)対称性
物理系が対称性を持つとは、その物理系を支配する法則が、対称変換に対して不変であることを言います。一般に物理法則が(連続的な)対称性を持つ時は、対応する保存量が存在することが知られています。例えば、エネルギー保存則と運動量保存則は、それぞれ時間と空間をずらしても物体の運動法則が変わらないという対称性に対応しています。量子力学においてはより複雑な対称性が多数あり、多彩な物理現象と関わっています。
(注3)熱力学第二法則
熱平衡状態を冷やしてその熱を仕事に変えるだけで、それ以外には何の変化も起こさないような第二種永久機関は存在しないことが、熱力学第二法則として確立しています。これはケルビンの原理とも呼ばれます。本研究では、ケルビンの原理を量子力学的に定式化することによって熱平衡状態を扱っています。
(注4)一般化ギブス分布
まずギブス分布(カノニカル分布)とは、熱平衡状態を量子力学的に記述する際に用いられる、最も標準的な状態の概念です。一般化ギブス分布とは、エネルギーや粒子数以外の保存量が存在する場合に、それらの保存量を取り入れてギブス分布を拡張したものです。ただし、これまでの一般化ギブス分布の研究の多くは、保存量が互いに可換な場合について扱っており、量子力学に特有の状況である非可換な場合についてはあまり研究がなされていませんでした。
(注5)非可換性
量子力学では、位置や運動量などの物理量は演算子で表されるため、二つの物理量の掛け算はその順序によって結果が異なります。そのような場合に、それらの物理量は互いに非可換であると言います。このことに起因して、量子力学においては例えば位置と運動量は同時に確定した値を取らないことなど、古典力学とは著しく異なる性質が現れます。
(注6)スピン
スピンとは電子などが持つ角運動量の一種であり、物質の磁性の起源となります。スピンは量子力学に特有の物理量で、向きの異なるスピンを表す演算子は互いに非可換となります。
7.添付資料: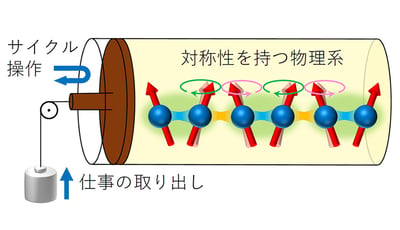 図1:量子力学的な対称性を持つ熱機関を考えます。その対称性を満たすサイクル操作によっては決して仕事を取り出せない時、状態は対称性によって保護された熱平衡状態と見なすことができます。本研究では、そのような状態は全て一般化ギブス分布と呼ばれる状態となることを証明しました。この結果は量子力学特有の状況にも適用できます。対称性に保護された熱平衡状態は、従来の熱力学における熱平衡状態の概念よりも広いため、より柔軟な量子熱機関の設計原理に繋がることが期待されます。
図1:量子力学的な対称性を持つ熱機関を考えます。その対称性を満たすサイクル操作によっては決して仕事を取り出せない時、状態は対称性によって保護された熱平衡状態と見なすことができます。本研究では、そのような状態は全て一般化ギブス分布と呼ばれる状態となることを証明しました。この結果は量子力学特有の状況にも適用できます。対称性に保護された熱平衡状態は、従来の熱力学における熱平衡状態の概念よりも広いため、より柔軟な量子熱機関の設計原理に繋がることが期待されます。
プレスリリース本文:PDFファイル
Physical Review X:https://journals.aps.org/prx/abstract/10.1103/PhysRevX.12.021013
おすすめ記事
本件に関連する記事はこちら
量子制御下での熱力学第二法則 〜量子情報と熱力学の融合に向けて〜
網羅的なトポロジカル超伝導物質探索へ向けた新データベースの構築