発表のポイント
◆ 統計力学の最も基本的な模型であるイジング模型の動的臨界指数が任意の空間次元で2以上であることを世界で初めて証明しました。
◆ 従来知られていた下限を数学的に厳密に改善し、数値結果との整合性をもつ下限を確立しました。この成果は、フラストレーションフリーな量子多体系の性質に基づいて古典統計力学系の非平衡ダイナミクスに対する制限を導いた点で、全く予想されていなかった発見です。
◆ 本成果は、動的臨界現象の理論的基盤を強化し、物性物理や材料科学におけるスピン系の緩和ダイナミクス解析への応用が期待されます。また、古典と量子を横断するアプローチにより、新たな理論物理の展開にも寄与することが期待されます。

臨界温度における磁性体の時間発展のシミュレーション
発表内容
東京大学大学院工学系研究科物理工学専攻の政岡凜太郎大学院生(修士課程2年)、渡辺悠樹准教授、および米ハーバード大学の副島智大研究員による研究グループは、古典統計力学の基本模型であるイジング模型(注1)における動的臨界指数(注2)zに対して、任意の空間次元で普遍的に成り立つ厳密な下限z ≥ 2を世界で初めて証明することに成功しました。この成果は、動的臨界現象(注3)の理解における100年来の未解決問題に対して、理論的なブレイクスルーを与えるものです。
イジング模型は、強磁性相転移の記述を目的として1925年にエルンスト・イジングの博士論文で提案された理論モデルです。その特筆すべき点は、単純な構造でありながら臨界現象や相転移といった複雑な現象を記述できることにあり、物理学のみならず情報科学、生物学、さらには社会科学にも応用されています。特に、2次元イジング模型は1944年にオンザガーによって厳密解が与えられ、統計力学の金字塔として知られています。2025年はその誕生からちょうど100年という節目の年にあたります。
今回対象としたのは、イジング模型のスピンの時間発展、すなわち緩和ダイナミクスを記述するために用いられる「動的イジング模型」です。このモデルでは、スピンの反転が確率的なルールに従って起こると仮定され、その一連の過程はマルコフ過程(注4)として記述されます。
臨界点近傍では、スピン系の緩和時間τが系のサイズLと共に発散的に増大する「臨界スローイングダウン」(注5)という現象が起こります。この発散を特徴づけるτ∼ Lzという関係により、動的臨界指数zが定義されます。これまでの理論的な知見では、2次元イジング模型に対してはz ≥ 1.75という不等式が示されていました。一方で数値的にはz ≥ 2.1667(5)と報告されており、理論と数値の間にギャップがありました。
このギャップを埋めるべく、研究グループは、最近独自に発展させたフラストレーションフリーな量子多体系(注6)に関する理論を出発点として、古典統計力学のマルコフ過程を対応する量子系に対応させる手法を用いました。その結果として、緩和時間τがL2/(logL )2以上で成長すること、すなわち動的臨界指数がz ≥ 2を満たすことを厳密に証明することに成功しました(図1)。この証明は、古典イジング模型の相関関数に対して従来知られていたSimon–Liebの不等式(注7)と、量子情報理論において近年確立されたDetectabilityに関する補題(注8)を用いて示されたGosset–Huangの不等式(注8)を巧みに組み合わせたものです。これは、量子と古典の物理を架橋する斬新なアプローチといえます。

図1:臨界温度における磁性体の時間発展のシミュレーション
マルコフ連鎖モンテカルロ法で臨界温度T=Tcにおける2次元動的イジング模型をシミュレーションした結果。黒と白は磁性体内部のスピンの向きを示し、縦軸が空間1次元の断面、横軸が時間を表す。ここでのzは、空間の大きさLに対して緩和にかかる時間がLz程度になることを定量化する動的臨界指数で、本研究ではその下限がz ≥ 2であることを示した。
本研究の意義は、単なる一つの不等式の導出にとどまりません。動的臨界指数は、材料科学におけるスピン緩和時間の評価、モンテカルロ法における収束速度の見積り、さらには非平衡系の理論構築など多方面に応用される基盤的な概念であり、その普遍的制限が明らかになったことで、今後の理論展開や実験設計の指針として重要な意味を持ちます。さらに、量子情報理論や多体量子物理の知見が古典統計力学に還元的に貢献するという点でも、学際的な波及効果が期待されます。
本研究成果は、2025年5月26日(現地時間)に国際物理学専門誌Journal of Statistical Physicsに掲載されました。
発表者・研究者等情報
東京大学 大学院工学系研究科
政岡 凜太郎 修士課程
兼:変革を駆動する先端物理・数学プログラム(FoPM) コース生
渡辺 悠樹 准教授
ハーバード大学 物理学科
副島 智大 研究員
論文情報
雑誌名:Journal of Statistical Physics
題 名:Rigorous lower bound of the dynamical critical exponent of the Ising model
著者名:Rintaro Masaoka, Tomohiro Soejima, Haruki Watanabe*
DOI:10.1007/s10955-025-03456-3
URL:https://link.springer.com/article/10.1007/s10955-025-03456-3(オープンアクセス)
研究助成
本研究は、科研費「超伝導体のゲージ不変な非線形応答理論の構築(課題番号:JP24K00541)」およびGordon and Betty Moore Foundation’s EPiQS Initiative(課題番号:GBMF8683)の支援により実施されました。
用語解説
(注1)イジング模型:スピンが格子点上に配置され、隣接スピン間の相互作用を考える統計力学の基本モデル。磁性や相転移現象の解析に広く用いられる。
(注2)動的臨界指数:臨界点近傍における緩和時間の系サイズ依存性τ∼ Lzを特徴づける指数で、系が平衡に達するまでの時間スケールを表す。
(注3)動的臨界現象:相転移点近傍で観測される、緩和時間の発散や時間スケールの異常な増大といった非平衡的挙動。
(注4)マルコフ過程:現在の状態のみが将来の状態に影響を与えるという性質(マルコフ性)を持つ確率過程。動的イジング模型の記述に用いられる。
(注5)臨界スローイングダウン:臨界点に近づくにつれて系の緩和が極端に遅くなる現象で、動的臨界指数によって定量化される。
(注6)フラストレーションフリーな量子多体系:ハミルトニアンの各項が同時に最小化される量子系で、基底状態の構造が解析しやすく、量子情報理論や統計物理において注目されている。
(注7)Simon–Liebの不等式:スピン系における相関関数の下限を与える不等式で、臨界点での長距離相関の存在を示す際に用いられる。
(注8)Detectabilityに関する補題とGosset–Huangの不等式:量子系のスペクトルギャップと相関長との関係を定量的に結びつける理論的道具で、今回の証明で相関関数の上限評価に使用された。
プレスリリース本文:PDFファイル
Journal of Statistical Physics:https://link.springer.com/article/10.1007/s10955-025-03456-3
おすすめ記事
本件に関連する記事はこちら
TVを上回るソーシャルメディアの自己訂正力 ―変異種から変異株へ、テレビより速いX(旧Twitter)上の科学用語の扱いの変化―
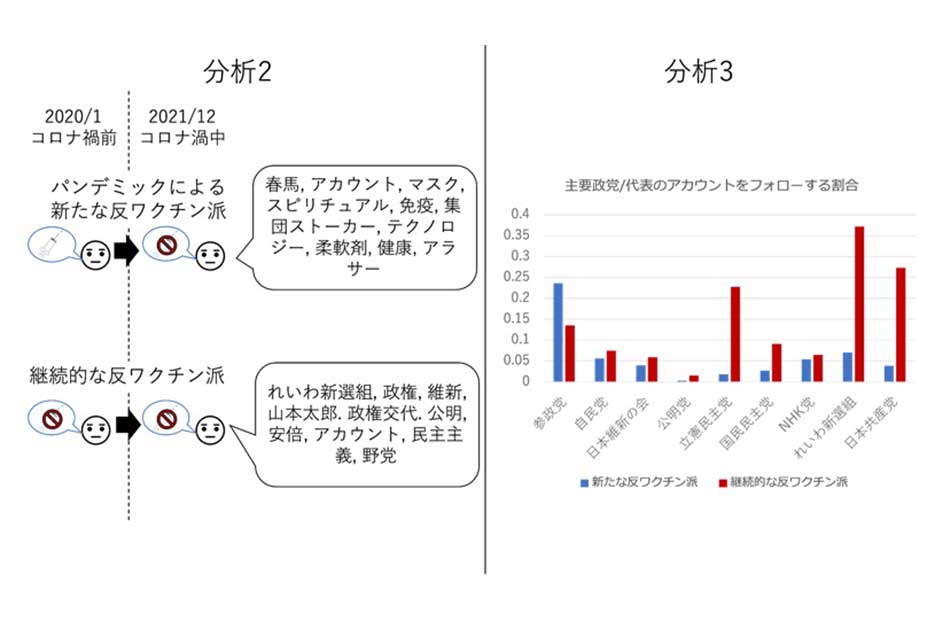
人はなぜワクチン反対派になるのか ―コロナ禍におけるワクチンツイートの分析―


