Share this
Young Faculty / 010
Associate Professor Takashi Goda,Sato, Kobayashi & Goda Lab., Department of Systems Innovation

<Biography>
2007.3: B.E., Depart. of Systems Innovation, U. Tokyo
2009.3: M.S., Depart. of Geosystems Engineering, U. Tokyo
2012.3: Dr.Eng., Depart. of Systems Innovation, U. Tokyo
2010.4-2012.3: Research Fellow (DC), Japan Society for the Promotion of Science
2012.4-2013.12: Research Fellow (PD), Japan Society for the Promotion of Science
2014.1-2015.2: Project Assist. Prof., School of Eng., U. Tokyo
2015.3-2017.3: Assist. Prof., Frontier Research Center for Energy and Resources, U. Tokyo
2017.4-: Assoc. Prof., Depart. of Systems Innovation, U. Tokyo
<About the Research>
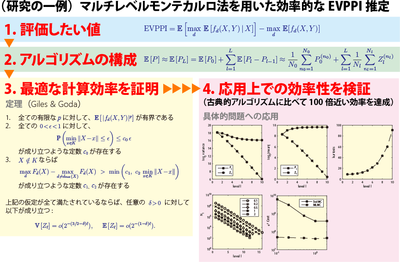
There are plenty of probabilistic events which cannot be deterministically predictable, such as natural phenomena and economic activities. I have been interested in how to evaluate those uncertainties in a quantitative manner and also in how to use such evaluation to make more rational decisions or to optimize system designs. As for uncertainty quantification, Monte Carlo methods have been widely used in practice, which simply generate lots of independent but equally probable scenarios and then compute some statistics of their outputs. While Monte Carlo methods are versatile in general, their computational efficiencies are not always good enough for some applications. As an alternative approach to classical Monte Carlo methods, I am focusing on quasi-Monte Carlo (QMC) and multilevel Monte Carlo (MLMC) methods, and investigating their theoretical foundations, construction of various algorithms, and applications to engineering problems, see for instance [1, 2]. Furthermore, I am currently working on measuring cost-effectiveness of reducing uncertainties in prediction, say, by gathering more information and data. The research field of medical decision making is particularly in need of appropriate cost-effectiveness analyses and efficient algorithms. However, the existing algorithms developed so far have some disadvantages; the computational efficiencies are quite bad or they have no mathematical proofs that they provide a right solution. Recently, together with Prof. Michael Giles at Oxford, I have successfully developed an efficient algorithm which theoretically achieves the optimal computational efficiency, and have shown the effectiveness in practical implementations [3].
[1] G. & Dick, Found. Comput. Math., 15 (2015), 1245-1278.
[2] G., Suzuki & Yoshiki, Found. Comput. Math., 18 (2018), 433-458.
[3] Giles & G., Stat. Comput., doi.org/10.1007/s11222-018-9835-1
<Future aprirations>
I am thinking of improving the performance of the developed algorithms further, and also of making them more versatile and generalized. At the same time, I want to implement the algorithms more user-friendly, so that non-experts can use them for various real applications without prior knowledge.
Takeshi Goda's home page: https://sites.google.com/site/takashigoda/home
These Related Stories
