Share this
Authors
Yuma Okazaki, Takehiko Oe, Minoru Kawamura, Ryutaro Yoshimi, Shuji Nakamura, Shintaro Takada, Masataka Mogi, Kei S. Takahashi, Atsushi Tsukazaki, Masashi Kawasaki, Yoshinori Tokura & Nobu-Hisa Kaneko
Abstract
The quantum anomalous Hall effect (QAHE)1,2,3,4,5,6 is a transport phenomenon where the Hall resistance is quantized to the von Klitzing constant due to the spontaneous magnetization of a ferromagnetic material even at zero magnetic field. Similar to the quantum Hall effect (QHE) under strong magnetic fields, the quantized Hall resistance of QAHE is supposed to be universal, independent of the details in the experimental realization7,8. However, the quantization accuracy of QAHE reported so far9,10,11 is much poorer than that of QHE. Here we demonstrate a precision of 10 parts per billion of Hall resistance quantization in QAHE. By directly comparing QAHE with QHE, we confirm that the quantization accuracy of QAHE satisfies the required level as a primary standard of electric resistance. We achieve this high accuracy of quantization by using a weak magnetic field supplied by a permanent disc magnet to align the magnetization domains. Our findings establish a milestone for developing a quantum resistance standard without strong magnetic fields.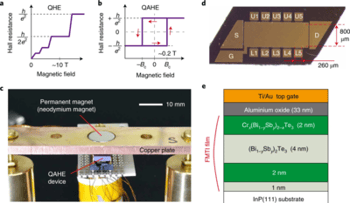
【References】
1.Yu, R. et al. Quantized anomalous Hall effect in magnetic topological insulators. Science 329, 61–64 (2010).
2.Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
3.Checkelsky, J. G. et al. Trajectory of the anomalous Hall effect towards the quantized state in a ferromagnetic topological insulator. Nat. Phys. 10, 731–736 (2014).
4.Kou, X. et al. Scale-invariant quantum anomalous Hall effect in magnetic topological insulators beyond the two-dimensional limit. Phys. Rev. Lett. 113, 199901 (2014).
5.Chang, C.-Z. et al. High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator. Nat. Mater. 14, 473–477 (2015).
6.Bestwick, A. J. et al. Precise quantization of the anomalous Hall effect near zero magnetic field. Phys. Rev. Lett. 114, 187201 (2015).
7.Jeckelmann, B. & Jeanneret, B. The quantum Hall effect as an electrical resistance standard. Rep. Prog. Phys. 64, 1603–1655 (2001).
8.Poirier, W. & Schopfer, F. Resistance metrology based on the quantum Hall effect. Eur. Phys. J. Spec. Top. 172, 207–245 (2009).
9.Götz, M. et al. Precision measurement of the quantized anomalous Hall resistance at zero magnetic field. Appl. Phys. Lett. 112, 072102 (2018).
10.Fox, E. J. et al. Part-per-million quantization and current-induced breakdown of the quantum anomalous Hall effect. Phys. Rev. B 98, 075145 (2018).
11.Okazaki, Y. et al. Precise resistance measurement of quantum anomalous Hall effect in magnetic heterostructure film of topological insulator. Appl. Phys. Lett. 116, 143101 (2020).
Nature Physics : https://www.nature.com/articles/s41567-021-01424-8
These Related Stories