Nonlinearity-induced topological phase transition characterized by the nonlinear Chern number

Authors

Kazuki Sone, Motohiko Ezawa, Yuto Ashida, Nobuyuki Yoshioka, Takahiro Sagawa

Abstract

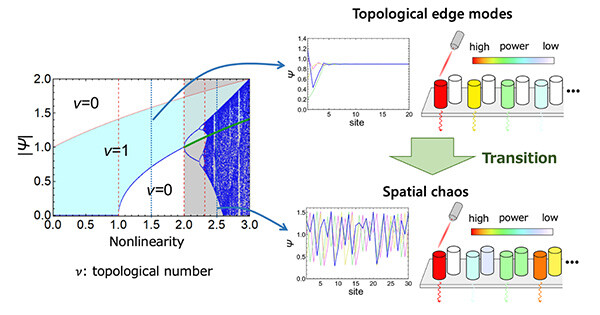
As first demonstrated by the characterization of the quantum Hall effect by the Chern number, topology provides a guiding principle to realize the robust properties of condensed-matter systems immune to the existence of disorder. The bulk–boundary correspondence guarantees the emergence of gapless boundary modes in a topological system whose bulk exhibits non-zero topological invariants. Although some recent studies have suggested a possible extension of the notion of topology to nonlinear systems, the nonlinear counterpart of a topological invariant has not yet been understood. Here we propose a nonlinear extension of the Chern number based on the nonlinear eigenvalue problems in two-dimensional systems and show the existence of bulk–boundary correspondence beyond the weakly nonlinear regime. Specifically, we find nonlinearity-induced topological phase transitions, in which the existence of topological edge modes depends on the amplitude of oscillatory modes. We propose and analyse a minimal model of a nonlinear Chern insulator whose exact bulk solutions are analytically obtained. The model exhibits the amplitude dependence of the nonlinear Chern number, for which we confirm the nonlinear extension of the bulk–boundary correspondence. Thus, our result reveals the existence of genuinely nonlinear topological phases that are adiabatically disconnected from the linear regime.

Nature Physics: https://www.nature.com/articles/s41567-024-02451-x