Share this
Authors
Minoru Kawamura, Masataka Mogi, Ryutaro Yoshimi, Takahiro Morimoto, Kei S. Takahashi, Atsushi Tsukazaki, Naoto Nagaosa, Masashi Kawasaki, and Yoshinori Tokura
Abstract
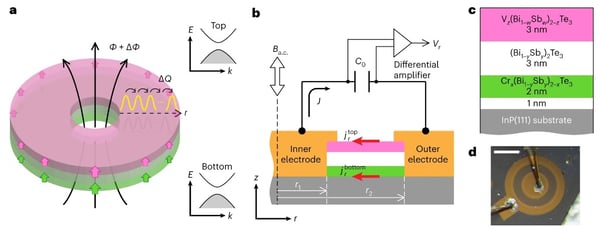
Adiabatic charge pumping is one of the most salient features of topological phases of matter1,2,3. Laughlin’s charge pumping in a quantum Hall system is the prototypical example4. In analogy, three-dimensional topological insulators have been predicted to support charge pumping through their magnetically gapped surface states5,6,7,8,9,10. But despite its importance as a direct probe of surface Hall conductivity, charge pumping has not been demonstrated in topological-insulator-based systems. Here we report the observation of charge pumping in a thin-film magnetic heterostructure of topological insulators in a geometry that prohibits edge transport. We find that charge pumping occurs between the inner and outer electrodes in response to alternating magnetic fields when the sample is in the quantum anomalous Hall insulator phase. The amount of pumped charge is accounted for by the surface Hall conductivity of half the quantum conductance for each surface, from a comparison with the axion insulator phase that shows no charge pumping. Because charge pumping is closely related to the theoretically predicted topological magnetoelectric effect5,6,7,8,9,10, our observation may provide clues to its direct observation.
References
Thouless, D. J. Quantization of particle transport. Phys. Rev. B 27, 6083–6087 (1983).
Lohse, M., Schweizer, C., Zilberberg, O., Aidelsburger, M. & Bloch, I. A Thouless quantum pump with ultracold bosonic atoms in an optical superlattice. Nat. Phys. 12, 350–354 (2016).
Nakajima, S. et al. Topological Thouless pumping of ultracold fermions. Nat. Phys. 12, 296–300 (2016).
Laughlin, R. B. Quantized Hall conductivity in two dimensions. Phys. Rev. B 23, 5632–5633 (1981).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Essin, A. M., Moore, J. E. & Vnderbilt, D. Magnetoelectric polarizability and axion electrodynamics in crystalline insulators. Phys. Rev. Lett. 102, 146805 (2009).
Essin, A. M., Turner, A. M., Moore, J. E. & Vanderbilt, D. Orbital magnetoelectric coupling in band insulators. Phys. Rev. B 81, 205104 (2010).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Sekine, A. & Nomura, K. Axion electrodynamics in topological materials. J. Appl. Phys. 129, 141101 (2021).
Nature Physics: https://www.nature.com/articles/s41567-022-01888-2
These Related Stories