Young Faculty / 002
Lecturer Asuka Hatano, Izumi & Hatano Lab., Department of Mechanical Engineering

<Biography>
Asuka Hatano received the B.S. degree from School of Engineering, the University of Tokyo in 2007, and the M.S. and Ph.D. degrees from Graduate School of Frontier Sciences, the university of Tokyo. After working for 5 years as assistant professor, she is now a Lecturer of Graduate School of Engineering at the University of Tokyo, since Mar. 2018.
<about the Research>
Multi-physics simulation of cardiomyocyte considering subcellular structures
Contraction of each cardiomyocyte produces the pumping of the heart. Cardiomyocytes have well-ordered intracellular structure. Disruption in structure often accompanied by a disorder of heart function, however, the causal relationship hasn't been elucidated.
Contraction of cardiomyocytes is a coupled problem of mechanical, electrical, and physiological phenomena because electrical activity at the cellular membrane triggers physiological reactions of ions and proteins, and reactions between actin and myosin result in contraction, and contraction changes diffusion distances, thus interact each other. The aim of my research is to gain medical insights on the effect of ultrastructure on myocardial contraction by realizing integrated simulation considering localized subcellular reactions, substrate supply with diffusion, excitation-contraction coupling, and mechanical contraction. You may question why cardiomyocyte, while belonging to the mechanical engineering department. The knowledge of mechanical engineering is fundamental to this multi-physics simulation.
Our cardiomyocyte model is based on the finite element method. To save the computational cost, we modeled 3 myofibrils of 1 sarcomere length, assuming the periodicity and the symmetricity of myocyte. (Figure 1) On this mesh, we solved reaction-diffusion equation for 7 ions solutes namely, Calcium ion (Ca2+), ATP, ADP, inorganic phosphate, Creatine, Creatine phosphate, and Oxygen. Diffusion term corresponds to transfer, and reaction term corresponds to uptake and release of each subcellular components, such as JSR, NSR, myofibril and so on. These reactions sites are located at the appropriate nodes to reproduce the anatomical structure.
Intracellular Ca2+ is signal of contraction. On excitation, Ca2+ concentration rises 10 times compared to the rest. Because Ca2+ is released only from sarcolemma and junctional SR, the intracellular Ca2+ gradient is steep. Our cardiomyocyte model reproduced temporal and spatial distribution Ca2+, together with electrical activity and contractile deformation. [Link: paper1]
I would like to introduce application to the case of t-tubule deletion. T-tubule is invagination of the membrane. Because electrical activation occurs at the membrane, this invagination synchronizes Ca2+ rise throughout the cell. In heart failure, deletion of t-tubule is observed, which we call detubulation. We examined the effect of detubulation using the model. Figure 2 shows Ca2+ propagation of control and detubulated model. In control model, Ca rises simultaneously, however in detubulated model Ca rises first at the surface membrane, and then propagates into the core region. Contraction also delayed in a detubulated model. [Link paper2] We also investigated the meaning of colocalization of mitochondria and Ca2+ release sites [link paper3] and the distance between mitochondria and sarcolemma [link paper4].
(Figure 1)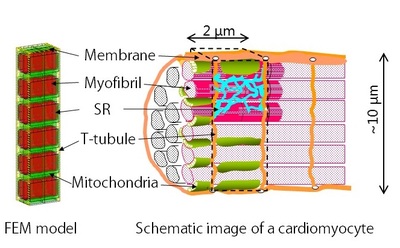
(Figure 2)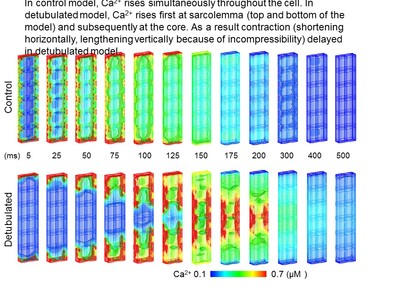
(Laboratory) http://www.fml.t.u-tokyo.ac.jp/
[link: paper1] http://www.sciencedirect.com/science/article/pii/S0006349511012392
[link: paper2] http://www.sciencedirect.com/science/article/pii/S0021929011007044
[link: paper3] http://www.cell.com/biophysj/abstract/S0006-3495(12)05113-2
[link: paper4] http://www.sciencedirect.com/science/article/pii/S000634951500449X
<Future aspirations>
At present, the shape of the model is geometric. The model often criticized 'UNrealistic'. The actual shape is complicated, there is regularity in randomness. How to incorporate this actual shape into the model and evolve it more realistic is my big issue in the future.
It is also our future goal to connect with a more microscopic model such as protein molecular dynamics calculations. I would like to contribute to the elucidation of the mechanism of myocardial contraction by simulation without black boxes.
Apart from this research, I also study the simulation of blood flow. As a researcher in the mechanical engineering department, I would like to continue working hard on applying simulation analysis in the medical field.
You May Also Like
These Related Stories

