Authors
M.Mogi, Y. Okamura, M. Kawamura, R. Yoshimi, K. Yasuda, A. Tsukazaki, K. S. Takahashi, T. Morimoto, N. Nagaosa, M. Kawasaki, Y. Takahashi, and Y. Tokura
Abstract
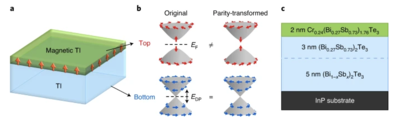
A three-dimensional (3D) topological insulator features a 2D surface state consisting of a single linearly dispersive Dirac cone1,2,3. Under broken time-reversal symmetry, the single Dirac cone is predicted to cause half-integer quantization of Hall conductance, which is a manifestation of the parity anomaly in quantum field theory1,2,3,4,5,6,7,8,9. However, despite various observations of quantization phenomena10,11,12,13,14,15, the half-integer quantization has not been observed because most experiments simultaneously measure a pair of equivalent Dirac cones16 on two opposing surfaces. Here we demonstrate the half-integer quantization of Hall conductance in a synthetic heterostructure termed a semi-magnetic topological insulator, where only one surface state is gapped by magnetic doping and the opposite one is non-magnetic and gapless. We observe half-quantized Faraday and Kerr rotations with terahertz magneto-optical spectroscopy and half-quantized Hall conductance in transport at zero magnetic field. Our results suggest a condensed-matter realization of the parity anomaly4,5,6,7,8,9 and open a way for studying the physics enabled by a single Dirac fermion.
【References】
1.Fu, L., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
2.Fu, L. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
3.Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
4.Niemi, A. J. & Semenoff, G. W. Axial-anomaly-induced fermion fractionization and effective gauge-theory actions in odd-dimensional space-times. Phys. Rev. Lett. 51, 2077–2080 (1983).
5.Redlich, A. N. Gauge noninvariance and parity nonconservation of three-dimensional fermions. Phys. Rev. Lett. 52, 18–21 (1984).
6.Jackiw, R. Fractional charge and zero modes for planer systems in a magnetic field. Phys. Rev. D 29, 2375–2377 (1984).
7.Semenoff, G. Condensed-matter simulation of a three-dimensional anomaly. Phys. Rev. Lett. 53, 2449–2452 (1984).
8.Fradkin, E., Dagotto, E. & Boyanovsky, D. Physical realization of the parity anomaly in condensed matter physics. Phys. Rev. Lett. 57, 2967–2970 (1986).
9.Haldane, F. D. M. Model for a quantum Hall effect without Landau levels: condensed-matter realization of the ‘parity anomaly’. Phys. Rev. Lett. 61, 2015–2018 (1988).
10.Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
11.Xu, Y. et al. Observation of topological surface state quantum Hall effect in an intrinsic three-dimensional topological insulator. Nat. Phys. 10, 956–963 (2014).
12.Yoshimi, R. et al. Quantum Hall states stabilized in semi-magnetic bilayers of topological insulators. Nat. Commun. 6, 8530 (2015).
13.Wu, L. et al. Quantized Faraday and Kerr rotation and axion electrodynamics of a 3D topological insulator. Science 354, 1124–1127 (2016).
14.Dziom, V. et al. Observation of the universal magnetoelectric effect in a 3D topological insulator. Nat. Commun. 8, 15197 (2017).
15.Okada, K. N. et al. Terahertz spectroscopy on Faraday and Kerr rotations in a quantum anomalous Hall state. Nat. Commun. 7, 12245 (2016).
16.Nielsen, N. B. & Ninomiya, M. Absence of neutrinos on a lattice: (I). Proof by homotopy theory. Nucl. Phys. B185, 20–40 (1981).
Nature Physics:https://www.nature.com/articles/s41567-021-01490-y
You May Also Like
These Related Stories
Quantum non-demolition detection of an itinerant microwave photon
Aggregation and collapse dynamics of skyrmions in a non-equilibrium state