Purifying Deep Boltzmann Machines for Thermal Quantum States

Authors
Yusuke Nomura, Nobuyuki Yoshioka, and Franco Nori

Abstract
We develop two cutting-edge approaches to construct deep neural networks representing the purified finite-temperature states of quantum many-body systems. Both methods commonly aim to represent the Gibbs state by a highly expressive neural-network wave function, exemplifying the idea of purification. The first method is an entirely deterministic approach to generate deep Boltzmann machines representing the purified Gibbs state exactly. This strongly assures the remarkable flexibility of the ansatz which can fully exploit the quantum-to-classical mapping. The second method employs stochastic sampling to optimize the network parameters such that the imaginary time evolution is well approximated within the expressibility of neural networks. Numerical demonstrations for transverse-field Ising models and Heisenberg models show that our methods are powerful enough to investigate the finite-temperature properties of strongly correlated quantum many-body systems, even when the problematic effect of frustration is present.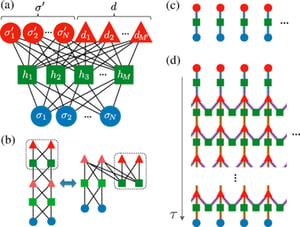

Physical Review Letters : https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.127.060601