PRESS RELEASE
- Research
- 2016
Self-optimized superconductivity attainable by interlayer phase separation at cuprate interfaces : Assistant Professor Takahiro Misawa (at the time Reserch) , Professor Masatoshi Imada, Department o
Authors
Takahiro Misawa, Yusuke Nomura, Silke Biermann, and Masatoshi Imada
Abstract
Stabilizing superconductivity at high temperatures and elucidating its mechanism have long been major challenges of materials research in condensed matter physics. Meanwhile, recent progress in nanostructuring offers unprecedented possibilities for designing novel functionalities. Above all, thin films of cuprate and iron-based high-temperature superconductors exhibit remarkably better superconducting characteristics (for example, higher critical temperatures) than in the bulk, but the underlying mechanism is still not understood. Solving microscopic models suitable for cuprates, we demonstrate that, at an interface between a Mott insulator and an overdoped nonsuperconducting metal, the superconducting amplitude is always pinned at the optimum achieved in the bulk, independently of the carrier concentration in the metal. This is in contrast to the dome-like dependence in bulk superconductors but consistent with the astonishing independence of the critical temperature from the carrier density x observed at the interfaces of La2CuO4 and La2−xSrxCuO4. Furthermore, we identify a self-organization mechanism as responsible for the pinning at the optimum amplitude: An emergent electronic structure induced by interlayer phase separation eludes bulk phase separation and inhomogeneities that would kill superconductivity in the bulk. Thus, interfaces provide an ideal tool to enhance and stabilize superconductivity. This interfacial example opens up further ways of shaping superconductivity by suppressing competing instabilities, with direct perspectives for designing devices.
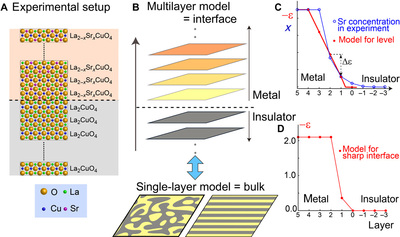
Experimental setup and present theoretical model of the cuprate interface. (A) Schematic experimental setup of the cuprate interface (2). (B) Top: Illustration of the interface model for cuprates. The dotted line denotes the interface between the metallic and the insulating layer. The color schematically illustrates the change in the carrier concentration obtained in the present work. Bottom: Two hypothetical bulk or single-layer phases with charge inhomogeneity within a layer. (C) Layer dependence of onsite energy level chosen to model the interface (red line). In the metallic phase, the onsite energy level is assumed to change linearly. This is an approximation that takes into account the effect of interlayer atomic diffusion [blue curve; taken from the study of Logvenov et al. (20)] combined with effects from the Madelung potential and the spatial extension of the Wannier orbital at the interface. (D) Onsite level of a sharp interface modeled by means of an ab initio calculation for x = 0.4.
Science Advances URL: http://advances.sciencemag.org/content/2/7/e1600664.full

